题目内容
2.极坐标方程为lgρ=1+lgcosθ,则曲线上的点(ρ,θ)的轨迹是(x-5)2+y2=25(x≠0)..分析 极坐标方程为lgρ=1+lgcosθ,化为ρ=10cosθ(cosθ>0),即ρ2=10ρcosθ,把$\left\{\begin{array}{l}{{ρ}^{2}={x}^{2}+{y}^{2}}\\{x=ρcosθ}\end{array}\right.$代入即可得出.
解答 解:极坐标方程为lgρ=1+lgcosθ,
化为ρ=10cosθ(cosθ>0),
化为ρ2=10ρcosθ,
∴x2+y2=10x,
配方为(x-5)2+y2=25.
表示为以(5,0)为圆心,5为半径的圆,去掉极点.
故答案为:(x-5)2+y2=25(x≠0).
点评 本题考查了圆的极坐标方程化为直角坐标方程,考查了推理能力与计算能力,属于基础题.

练习册系列答案
 智趣暑假温故知新系列答案
智趣暑假温故知新系列答案
相关题目
17.已知区域Ω1={(x,y)|0≤y≤$\sqrt{9-{x}^{2}}$},区域Ω2={(x,y)|(x+3)(x-y+3)≤0},若向区域Ω1内随机投一点Q,则点Q落在区域Ω2内的概率为( )
| A. | $\frac{π-2}{2π}$ | B. | $\frac{π+2}{2π}$ | C. | $\frac{π+2}{4π}$ | D. | $\frac{π-2}{4π}$ |
14.“a=0”是“直线l1:x+ay-a=0与l2:ax-(2a-3)y-1=0”垂直的( )
| A. | 必要不充分条件 | B. | 充分不必要条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
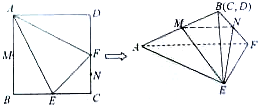 在边长为4的正方形ABCD中,E、F分别是BC、CD的中点,M、N分别是AB、CF的中点,将该正方形沿AE、AF、EF折叠,使B、C、D三点重合,构成一个三棱锥,如图所示.
在边长为4的正方形ABCD中,E、F分别是BC、CD的中点,M、N分别是AB、CF的中点,将该正方形沿AE、AF、EF折叠,使B、C、D三点重合,构成一个三棱锥,如图所示.
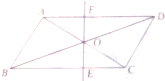 如图,平行四边形ABCD中,AB⊥AC,AB=1,BC=$\sqrt{5}$,对角线AC,BD相交于点O,将直线AC绕点O顺时针旋转,分别交BC、AD于点E、F.
如图,平行四边形ABCD中,AB⊥AC,AB=1,BC=$\sqrt{5}$,对角线AC,BD相交于点O,将直线AC绕点O顺时针旋转,分别交BC、AD于点E、F.