题目内容
12.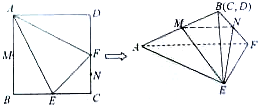 在边长为4的正方形ABCD中,E、F分别是BC、CD的中点,M、N分别是AB、CF的中点,将该正方形沿AE、AF、EF折叠,使B、C、D三点重合,构成一个三棱锥,如图所示.
在边长为4的正方形ABCD中,E、F分别是BC、CD的中点,M、N分别是AB、CF的中点,将该正方形沿AE、AF、EF折叠,使B、C、D三点重合,构成一个三棱锥,如图所示.(1)证明:MN∥平面AEF;
(2)证明:AB⊥平面BEF;
(3)求四棱锥E-AFNM的体积.
分析 (1)折叠后的图形:△ABF中,由M、N分别是AB、BF的中点,可得MN∥AF,即可证明MN∥平面AEF;
(2)在正方形ABCD中,AB⊥BE,AD⊥DF,折叠后的图形B,C,D三点重合,即可证明AB⊥平面BEF.
(3):VA-BEF=$\frac{1}{3}AB•{S}_{△BEF}$.而$\frac{{S}_{△BMN}}{{S}_{△ABF}}$=$\frac{1}{4}$,可得VE-AFNM=$\frac{3}{4}{V}_{A-BEF}$.
解答 (1)证明:折叠后的图形:△ABF中,
∵M、N分别是AB、BF的中点,
∴MN∥AF,MN?平面AEF,AF?平面AEF,
∴MN∥平面AEF;
(2)证明:在正方形ABCD中,AB⊥BE,AD⊥DF,折叠后的图形B,C,D三点重合,
∴三棱锥中,AB⊥BE,AB⊥BF,BE∩BF=B,
∴AB⊥平面BEF.
(3)解:VA-BEF=$\frac{1}{3}AB•{S}_{△BEF}$=$\frac{1}{3}×4×\frac{1}{2}×{2}^{2}$=$\frac{8}{3}$.
∵$\frac{{S}_{△BMN}}{{S}_{△ABF}}$=$\frac{1}{4}$,
∴VE-AFNM=$\frac{3}{4}{V}_{A-BEF}$=$\frac{3}{4}×\frac{8}{3}$=2.
点评 本题考查了正方形的性质、线面垂直的判定与性质定理、线面平行的判定定理、三角形中位线定理、三棱锥与四棱锥的体积计算公式,考查了空间想象能力,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
20.已知集合A={x∈Z|-1≤x≤2},集合B={y|y=sin$\frac{πx}{2}$},则A∩B=( )
| A. | {-1,0,1} | B. | {0,1,2} | C. | {-1,0,1,2} | D. | ∅ |
7.下面是关于复数z=$\frac{2}{1-i}$的四个命题:p1:|z|=2,p2:z2=2i,p3:z的共轭复数为-1+i,p4:z的虚部为1,其中真命题为( )
| A. | p2,p3 | B. | p1,p2 | C. | p2,p4 | D. | p3,p4 |
17.执行如图所示的程序框图,输出的S值为( )


| A. | 32 | B. | 50 | C. | 70 | D. | 90 |
4.在△ABC中,角A、B的对边分别为a、b且A=2B,sinB=$\frac{3}{5}$,则$\frac{a}{b}$的值是( )
| A. | $\frac{3}{5}$ | B. | $\frac{4}{5}$ | C. | $\frac{4}{3}$ | D. | $\frac{8}{5}$ |