题目内容
10.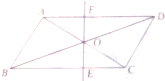 如图,平行四边形ABCD中,AB⊥AC,AB=1,BC=$\sqrt{5}$,对角线AC,BD相交于点O,将直线AC绕点O顺时针旋转,分别交BC、AD于点E、F.
如图,平行四边形ABCD中,AB⊥AC,AB=1,BC=$\sqrt{5}$,对角线AC,BD相交于点O,将直线AC绕点O顺时针旋转,分别交BC、AD于点E、F.(1)证明:当旋转角为90°时,四边形ABEF是平行四边形;
(2)试说明在旋转过程中,线段AF与EC总保持相等,在旋转过程中,四边形BEDF可能是菱形吗,如果不可能,请说明理由,如果可能,画出图形并写出此时AC绕点O顺时针旋转的度数.
分析 (1)根据垂直的定义可得∠BAO=90°,然后求出∠BAO=∠AOF,再根据内错角相等,两直线平行可得AB∥EF,然后根据平行四边形的对边平行求出AF∥BE,再根据两组对边分别平行的四边形是平行四边形证明;
(2)根据平行四边形的对边平行可得AD∥BC,对角线互相平分可得OA=OC,再根据两直线平行,内错角相等求出∠1=∠2,然后利用“角边角”证明△AOF和△COE全等,根据全等三角形对应边相等即可得到AF=CE;求出DF∥BE,DF=BE,然后根据一组对边平行且相等的四边形是平行四边形求出四边形BEDF平行四边形,再求出对角线互相垂直的平行四边形是菱形可得EF⊥BD时,四边形BEDF是菱形;根据勾股定理列式求出AC=2,再根据平行四边形的对角线互相平分求出AO=1,然后求出∠AOB=45°,再根据旋转的定义求出旋转角即可.
解答 (1)证明:当∠AOF=90°时,AB∥EF,
又∵AF∥BE,
∴四边形ABEF为平行四边形;(2分)
(2)解:四边形BEDF可以是菱形.
如图,连接BF,DE,∵四边形ABCD为平行四边形,
在△AOF和△COE中,$\left\{\begin{array}{l}{∠FAO=∠ECO}\\{AO=CO}\\{∠AOF=∠COE}\end{array}\right.$,
∴△AOF≌△COE(ASA),
∴AF=EC,OE=OF,
∴EF与BD互相平分.
∴当EF⊥BD时,四边形BEDF为菱形.(6分)
在Rt△ABC中,AC=2,∴OA=1=AB,
又∵AB⊥AC,
∴∠AOB=45°,(7分)
∴∠AOF=45°,
∴AC绕点O顺时针旋转45°时,四边形BEDF为菱形.(9分)
点评 本题考查了旋转的性质,平行四边形的判定与性质,全等三角形的判定与性质,菱形的判定与性质,综合题,但难度不大,熟练掌握平行四边形,菱形的联系与区别是解题的关键.

| A. | {-1,0,1} | B. | {0,1,2} | C. | {-1,0,1,2} | D. | ∅ |
| A. | {1,4,5} | B. | {4} | C. | {1,5} | D. | { 1,2,3,4,5} |
| A. | (-$\frac{3}{5}$,$\frac{4}{5}$) | B. | (-$\frac{4}{5}$,$\frac{3}{5}$) | C. | ($\frac{3}{5}$,-$\frac{4}{5}$) | D. | ($\frac{4}{5}$,-$\frac{3}{5}$) |
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |