题目内容
4.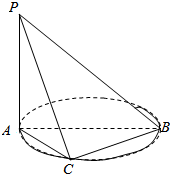 已知三棱锥P-ABC,C是以AB为直径的圆周上异于A、B的任一点,PA⊥平面ABC,PA=AB=2
已知三棱锥P-ABC,C是以AB为直径的圆周上异于A、B的任一点,PA⊥平面ABC,PA=AB=2(1)求证:BC⊥平面PAC
(2)求三棱锥P-ABC体积的最大值.
分析 (1)根据已知中PA垂直平面ABC,AB是⊙O的直径,易得PA⊥BC,BC⊥AC,我们易结合线面垂直的判定定理得到BC⊥面PAC
(2)表示出三棱锥P-ABC的体积,利用基本不等式,即可求三棱锥P-ABC体积的最大值.
解答 (1)证明:(1)∵PA⊥平面ABC,且BC?平面ABC,
∴PA⊥BC,
∵AB为⊙O的直径,∴BC⊥AC,
而PA∩AC=A
∴BC⊥面PAC
(2)解:设AC=x,则BC=$\sqrt{4-{x}^{2}}$,
∴VP-ABC=$\frac{1}{3}•\frac{1}{2}•$$\sqrt{4-{x}^{2}}$•2=$\frac{1}{3}$x$\sqrt{4-{x}^{2}}$=$\frac{1}{3}$$\sqrt{{x}^{2}(4-{x}^{2})}$≤$\frac{4}{9}$,
当且仅当x2=4-x2,取等号,
∴AC=$\sqrt{2}$时,三棱锥P-ABC体积的最大值为$\frac{4}{9}$.
点评 本题考查的知识点是直线与平面垂直的判定,三棱锥体积的计算,其中熟练掌握空间线面垂直的判定、性质,善于根据直角三角形、圆周角的性质,判断出直线与直线垂直是解答本题的关键.

练习册系列答案
 特高级教师点拨系列答案
特高级教师点拨系列答案
相关题目
15.已知f(x)=$\frac{1}{x}$,则f′(1)=( )
| A. | 0 | B. | 1 | C. | -1 | D. | -2 |
6.计划展出10幅不同的画,其中1幅水彩画、4幅油画、5幅国画,排成一列,要求同一品种的画必须连在一起,并且水彩画不放在两端,那么不同的排列方式的种数有( )
| A. | A44A55 | B. | A23A44A53 | C. | C31A44A55 | D. | A22A44A55 |