ΧβΡΩΡΎ»ί
ΓΨΧβΡΩΓΩ¬―–ΈœΏ «≥ΘΦϊ«ζœΏΒΡ“Μ÷÷Θ§Ζ÷Β―Ω®Εϊ¬―–ΈœΏΚΆΩ®ΈςΡα¬―–ΈœΏΘ§Ω®ΈςΡα¬―–ΈœΏ «ΤΫΟφΡΎ”κΝΫΗωΕ®ΒψΘ®Ϋ–ΫΙΒψΘ©ΒΡΨύάκ÷°ΜΐΒ»”Ύ≥Θ ΐΒΡΒψΒΡΙλΦΘΘ°Ρ≥Ά§―ßάύ±»Ά÷‘≤”κΥΪ«ζœΏΕ‘Ω®ΈςΡα¬―–ΈœΏΫχ––ΝΥœύΙΊ–‘÷ ΒΡΧΫΨΩΘ§…ηF1Θ®©¹cΘ§0Θ©Θ§F2Θ®cΘ§0Θ© «ΤΫΟφΡΎΒΡΝΫΗωΕ®ΒψΘ§|PF1||PF2|ΘΫa2Θ®a «≥Θ ΐΘ©Θ°ΒΟ≥ωΩ®ΈςΡα¬―–ΈœΏΒΡœύΙΊΫα¬έΘΚΔΌΗΟ«ζœΏΦ» «÷αΕ‘≥ΤΆΦ–Έ“≤ «÷––ΡΕ‘≥ΤΆΦ–ΈΘΜΔΎ»τaΘΫcΘ§‘ρ«ζœΏΙΐ‘≠ΒψΘΜΔέ»τ0ΘΦaΘΦcΘ§ΤδΙλΦΘΈΣœΏΕΈΘ°Τδ÷–’ΐ»ΖΟϋΧβΒΡ–ρΚ≈ «_____Θ°
ΓΨ¥πΑΗΓΩΔΌΔΎ
ΓΨΫβΈωΓΩ
…η![]() Θ§ΒΟΒΫ
Θ§ΒΟΒΫ![]() Θ§ΒΟΒΫ
Θ§ΒΟΒΫ![]() Θ§‘ΌΕ‘»ΐΗω―ΓœνΦ”“‘―ι÷ΛΘ§Φ¥Ω…«σΫβΘ§ΒΟΒΫ¥πΑΗ.
Θ§‘ΌΕ‘»ΐΗω―ΓœνΦ”“‘―ι÷ΛΘ§Φ¥Ω…«σΫβΘ§ΒΟΒΫ¥πΑΗ.
”…Χβ“β…ηPΘ®xΘ§yΘ©Θ§‘ρ![]() Θ§
Θ§
Φ¥[Θ®x+cΘ©2+y2][Θ®x©¹cΘ©2+y2]ΘΫa4Θ§
Ε‘”ΎΔΌ÷–Θ§“ρΈΣΑ―ΖΫ≥Χ÷–ΒΡx±Μ©¹x¥ζΜΜΘ§ΖΫ≥Χ≤Μ±δΘ§Ι ¥Υ«ζœΏΙΊ”Ύy÷αΕ‘≥ΤΘΜ
Α―ΖΫ≥Χ÷–ΒΡy±Μ©¹y ¥ζΜΜΘ§ΖΫ≥Χ≤Μ±δΘ§Ι ¥Υ«ζœΏΙΊ”Ύx÷αΕ‘≥ΤΘΜ
Α―ΖΫ≥Χ÷–ΒΡx±Μ©¹x¥ζΜΜΘ§y±Μ©¹y ¥ζΜΜΘ§ΖΫ≥Χ≤Μ±δΘ§
Ι ¥Υ«ζœΏ «÷αΕ‘≥ΤΆΦ–Έ“≤ «÷––ΡΕ‘≥ΤΆΦ–ΈΘ§Υυ“‘ «’ΐ»ΖΒΡΘ°
Ε‘”ΎΔΎ÷–Θ§»τaΘΫcΘ§Θ®0Θ§0Θ©¥ζ»κΘ§ΖΫ≥Χ≥…ΝΔ‘ρ«ζœΏΙΐ‘≠ΒψΘ§Υυ“‘ «’ΐ»ΖΒΡΘΜ
Ε‘”ΎΔέ÷–Θ§“ρΈΣΘ®|PF1|+|PF2|Θ©minΘΫ2cΘ§Θ®Β±«“ΫωΒ±Θ§|PF1|ΘΫ|PF2|ΘΫc ±»ΓΒ»Κ≈Θ©Θ§
Υυ“‘Θ®|PF1||PF2|Θ©minΘΫc2Θ§Υυ“‘»τ0ΘΦaΘΦcΘ§‘ρ«ζœΏ≤Μ¥φ‘ΎΘ§Υυ“‘≤Μ’ΐ»ΖΘ°
Ι ¥πΑΗΈΣΘΚΔΌΔΎ

ΓΨΧβΡΩΓΩΡ≥¥σ―ßΈΣΒς―–―ß…ζ‘Ύ![]() Θ§
Θ§ ![]() ΝΫΦ“≤ΆΧϋ”Ο≤ΆΒΡ¬ζ“βΕ»Θ§¥”‘Ύ
ΝΫΦ“≤ΆΧϋ”Ο≤ΆΒΡ¬ζ“βΕ»Θ§¥”‘Ύ![]() Θ§
Θ§ ![]() ΝΫΦ“≤ΆΧϋΕΦ”ΟΙΐ≤ΆΒΡ―ß…ζ÷–ΥφΜζ≥ι»ΓΝΥ100»ΥΘ§ΟΩ»ΥΖ÷±πΕ‘’βΝΫΦ“≤ΆΧϋΫχ––ΤάΖ÷Θ§¬ζΖ÷ΨυΈΣ60Ζ÷.
ΝΫΦ“≤ΆΧϋΕΦ”ΟΙΐ≤ΆΒΡ―ß…ζ÷–ΥφΜζ≥ι»ΓΝΥ100»ΥΘ§ΟΩ»ΥΖ÷±πΕ‘’βΝΫΦ“≤ΆΧϋΫχ––ΤάΖ÷Θ§¬ζΖ÷ΨυΈΣ60Ζ÷.
’ϊάμΤάΖ÷ ΐΨίΘ§ΫΪΖ÷ ΐ“‘10ΈΣΉιΨύΖ÷≥…6ΉιΘΚ ![]() Θ§
Θ§ ![]() Θ§
Θ§ ![]() Θ§
Θ§ ![]() Θ§
Θ§ ![]() Θ§
Θ§ ![]() Θ§ΒΟΒΫ
Θ§ΒΟΒΫ![]() ≤ΆΧϋΖ÷ ΐΒΡΤΒ¬ Ζ÷≤Φ÷±ΖΫΆΦΘ§ΚΆ
≤ΆΧϋΖ÷ ΐΒΡΤΒ¬ Ζ÷≤Φ÷±ΖΫΆΦΘ§ΚΆ![]() ≤ΆΧϋΖ÷ ΐΒΡΤΒ ΐΖ÷≤Φ±μΘΚ
≤ΆΧϋΖ÷ ΐΒΡΤΒ ΐΖ÷≤Φ±μΘΚ
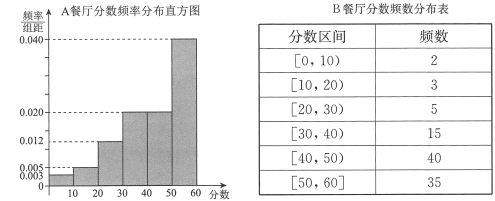
Ε®“ε―ß…ζΕ‘≤ΆΧϋΤάΦέΒΡΓΑ¬ζ“βΕ»÷Η ΐΓ±»γœ¬ΘΚ
Ζ÷ ΐ |
|
|
|
¬ζ“βΕ»÷Η ΐ |
|
|
|
Θ®ΔώΘ©‘Ύ≥ι―υΒΡ100»Υ÷–Θ§«σΕ‘![]() ≤ΆΧϋΤάΦέΓΑ¬ζ“βΕ»÷Η ΐΓ±ΈΣ0ΒΡ»Υ ΐΘΜ
≤ΆΧϋΤάΦέΓΑ¬ζ“βΕ»÷Η ΐΓ±ΈΣ0ΒΡ»Υ ΐΘΜ
Θ®ΔρΘ©¥”ΗΟ–Θ‘ΎΘ§ ![]() ΝΫΦ“≤ΆΧϋΕΦ”ΟΙΐ≤ΆΒΡ―ß…ζ÷–ΥφΜζ≥ι»Γ1»ΥΫχ––Βς≤ιΘ§ ‘ΙάΦΤΤδΕ‘
ΝΫΦ“≤ΆΧϋΕΦ”ΟΙΐ≤ΆΒΡ―ß…ζ÷–ΥφΜζ≥ι»Γ1»ΥΫχ––Βς≤ιΘ§ ‘ΙάΦΤΤδΕ‘![]() ≤ΆΧϋΤάΦέΒΡΓΑ¬ζ“βΕ»÷Η ΐΓ±±»Ε‘
≤ΆΧϋΤάΦέΒΡΓΑ¬ζ“βΕ»÷Η ΐΓ±±»Ε‘![]() ≤ΆΧϋΤάΦέΒΡΓΑ¬ζ“βΕ»÷Η ΐΓ±ΗΏΒΡΗ≈¬ ΘΜ
≤ΆΧϋΤάΦέΒΡΓΑ¬ζ“βΕ»÷Η ΐΓ±ΗΏΒΡΗ≈¬ ΘΜ
Θ®ΔσΘ©»γΙϊ¥”![]() Θ§
Θ§ ![]() ΝΫΦ“≤ΆΧϋ÷–―Γ‘ώ“ΜΦ“”Ο≤ΆΘ§ΡψΜα―Γ‘ώΡΡ“ΜΦ“ΘΩΥΒΟςάμ”….
ΝΫΦ“≤ΆΧϋ÷–―Γ‘ώ“ΜΦ“”Ο≤ΆΘ§ΡψΜα―Γ‘ώΡΡ“ΜΦ“ΘΩΥΒΟςάμ”….
ΓΨΧβΡΩΓΩΈΣΝΥ―ΓΑΈ―ß…ζ≤ΈΦ”»Ϊ –÷–―ß…ζΈοάμΨΚ»ϋΘ§―ß–Θœ»¥”ΗΏ»ΐΡξΦΕ―Γ»Γ60ΟϊΆ§―ßΫχ––ΨΚ»ϋ‘Λ―Γ»ϋΘ§ΫΪ≤ΈΦ”‘Λ―Γ»ϋΒΡ―ß…ζ≥…Φ®Θ®ΒΞΈΜΘΚΖ÷Θ©Α¥ΖΕΈß![]() Θ§
Θ§![]() Θ§
Θ§![]() Θ§
Θ§![]() Ζ÷ΉιΘ§ΒΟΒΫΒΡΤΒ¬ Ζ÷≤Φ÷±ΖΫΆΦ»γΆΦΘΚ
Ζ÷ΉιΘ§ΒΟΒΫΒΡΤΒ¬ Ζ÷≤Φ÷±ΖΫΆΦ»γΆΦΘΚ

Θ®1Θ©ΦΤΥψ’β¥Έ‘Λ―Γ»ϋΒΡΤΫΨυ≥…Φ®Θ®Ά§“ΜΉι÷–ΒΡ ΐΨί”ΟΗΟΉι«χΦδΒΡ÷–Βψ÷ΒΉς¥ζ±μΘ©ΘΜ
Θ®2Θ©»τΕ‘ΒΟΖ÷‘Ύ«Α![]() ΒΡ―ß…ζΫχ–––ΘΡΎΫ±άχΘ§ΙάΦΤΜώΫ±Ζ÷ ΐœΏΘΜ
ΒΡ―ß…ζΫχ–––ΘΡΎΫ±άχΘ§ΙάΦΤΜώΫ±Ζ÷ ΐœΏΘΜ
Θ®3Θ©»τ’β60Οϊ―ß…ζ÷–Ρ–≈°…ζ±»άΐΈΣ![]() Θ§≥…Φ®≤ΜΒΆ”Ύ60Ζ÷ΤάΙάΈΣΓΑ≥…Φ®ΝΦΚΟΓ±Θ§Ζώ‘ρΤάΙάΈΣΓΑ≥…Φ®“ΜΑψΓ±Θ§ ‘Άξ≥…œ¬Οφ
Θ§≥…Φ®≤ΜΒΆ”Ύ60Ζ÷ΤάΙάΈΣΓΑ≥…Φ®ΝΦΚΟΓ±Θ§Ζώ‘ρΤάΙάΈΣΓΑ≥…Φ®“ΜΑψΓ±Θ§ ‘Άξ≥…œ¬Οφ![]() Ν–ΝΣ±μΘ§ «Ζώ”–
Ν–ΝΣ±μΘ§ «Ζώ”–![]() ΒΡΑ―Έ’»œΈΣΓΑ≥…Φ®ΝΦΚΟΓ±”κΓΑ–‘±πΓ±”–ΙΊΘΩ
ΒΡΑ―Έ’»œΈΣΓΑ≥…Φ®ΝΦΚΟΓ±”κΓΑ–‘±πΓ±”–ΙΊΘΩ
≥…Φ®ΝΦΚΟ | ≥…Φ®“ΜΑψ | ΚœΦΤ | |
Ρ–…ζ | |||
≈°…ζ | |||
ΚœΦΤ |
ΗΫΘΚ![]() Θ§
Θ§![]()
ΝΌΫγ÷Β±μΘΚ
| 0.10 | 0.05 | 0.010 |
| 2.706 | 3.841 | 6.635 |
