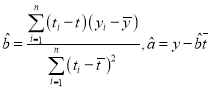题目内容
【题目】在平面直线坐标系中,定义![]() 为两点
为两点![]() 的“切比雪夫距离”,又设点P及
的“切比雪夫距离”,又设点P及![]() 上任意一点Q,称
上任意一点Q,称![]() 的最小值为点P到直线
的最小值为点P到直线![]() 的“切比雪夫距离”记作
的“切比雪夫距离”记作![]() 给出下列四个命题:( )
给出下列四个命题:( )
①对任意三点A、B、C,都有![]()
②已知点P(3,1)和直线![]() 则
则![]()
③到定点M的距离和到M的“切比雪夫距离”相等点的轨迹是正方形;
④定点![]() 动点
动点![]() 满足
满足![]() 则点P的轨迹与直线
则点P的轨迹与直线![]() (
(![]() 为常数)有且仅有2个公共点。
为常数)有且仅有2个公共点。
其中真命题的个数是( )
A.4B.3C.2D.1
【答案】A
【解析】
①讨论![]() ,
,![]() ,
,![]() 三点共线,以及不共线的情况,结合图象和新定义,即可判断;
三点共线,以及不共线的情况,结合图象和新定义,即可判断;
②运用新定义,求得点的轨迹方程,即可判断;
③设点![]() 是直线
是直线![]() 上一点,且
上一点,且![]() ,可得
,可得![]() ,
,![]() ,讨论
,讨论![]() ,
,![]() 的大小,可得距离
的大小,可得距离![]() ,再由函数的性质,可得最小值;
,再由函数的性质,可得最小值;
④讨论![]() 在坐标轴上和各个象限的情况,求得轨迹方程,即可判断.
在坐标轴上和各个象限的情况,求得轨迹方程,即可判断.
解:①对任意三点![]() 、
、![]() 、
、![]() ,若它们共线,设
,若它们共线,设![]() ,
,![]() 、
、![]() ,
,![]() ,
,
![]() ,
,![]() ,如右图,结合三角形的相似可得
,如右图,结合三角形的相似可得![]() ,
,![]() ,
,![]()
为![]() ,
,![]() ,
,![]() ,或
,或![]() ,
,![]() ,
,![]() ,则
,则![]() ,
,![]() ,
,![]() ,
,![]() ;
;
若![]() ,
,![]() 或
或![]() ,
,![]() 对调,可得
对调,可得![]() ,
,![]() ,
,![]() ,
,![]() ;
;

若![]() ,
,![]() ,
,![]() 不共线,且三角形中
不共线,且三角形中![]() 为锐角或钝角,由矩形
为锐角或钝角,由矩形![]() 或矩形
或矩形![]() ,
,
![]() ,
,![]() ,
,![]() ,
,![]() ;
;
则对任意的三点![]() ,
,![]() ,
,![]() ,都有
,都有![]() ,
,![]() ,
,![]() ,
,![]() ;故①正确;
;故①正确;
②到原点的“切比雪夫距离”等于1的点,即为![]() ,
,![]() ,若
,若![]() ,则
,则![]() ;
;
若![]() ,则
,则![]() ,故所求轨迹是正方形,则②正确;
,故所求轨迹是正方形,则②正确;
③设点![]() 是直线
是直线![]() 上一点,且
上一点,且![]() ,
,
可得![]() ,
,![]() ,
,
由![]() ,解得
,解得![]() ,即有
,即有![]() ,
,
当![]() 时,取得最小值
时,取得最小值![]() ;
;
由![]() ,解得
,解得![]() 或
或![]() ,即有
,即有![]() ,
,
![]() 的范围是
的范围是![]() ,
,![]() ,
,![]() ,
,![]() .无最值,
.无最值,
综上可得,![]() ,
,![]() 两点的“切比雪夫距离”的最小值为
两点的“切比雪夫距离”的最小值为![]() .
.
故③正确;
④定点![]() 、
、![]() ,动点
,动点![]()
满足![]() ,
,![]() ,
,![]() ,
,
可得![]() 不
不![]() 轴上,
轴上,![]() 在线段
在线段![]() 间成立,
间成立,
可得![]() ,解得
,解得![]() ,
,
由对称性可得![]() 也成立,即有两点
也成立,即有两点![]() 满足条件;
满足条件;
若![]() 在第一象限内,满足
在第一象限内,满足![]() ,
,![]() ,
,![]() ,
,

即为![]() ,为射线,
,为射线,
由对称性可得在第二象限、第三象限和第四象限也有一条射线,
则点![]() 的轨迹与直线
的轨迹与直线![]()
![]() 为常数)有且仅有2个公共点.
为常数)有且仅有2个公共点.
故④正确;
故选:![]()


【题目】某商店为迎接端午节,推出两款粽子:花生粽和肉粽.为调查这两款粽子的受欢迎程度,店员连续10天记录了这两种粽子的销售量,如下表表示(其中销售单位:个)
天数 销售量
天数 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 |
花生粽 | 103 | 93 | 98 | 93 | 106 | 86 | 87 | 94 | 91 | 99 | 100 |
肉粽 | 88 | 97 | 98 | 95 | 101 | 98 | 103 | 106 | 103 | 111 | 100 |
(1)根据两组数据完成下面茎叶图:
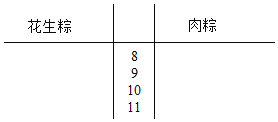
(2)统计学知识,请评述哪款粽子更受欢迎;
(3)求肉粽销售量y关于天数t的线性回归方程,并预估第15天肉粽的销售量(回归方程系数精确到0.1)
参考数据:![]() ,参考公式:
,参考公式: