Question

【题目】设函数，其中N，≥2，且R．

（1）当，时，求函数的单调区间；

（2）当时，令，若函数有两个极值点，，且，求的取值范围；

（3）当时，试求函数的零点个数，并证明你的结论．

Answer 1

【答案】（1）见解析；（2）；（3）见解析

【解析】

（1）将，代入解析式，求出函数的导数，从而即可得到函数的单调区间；

（2）由题意知，求导，从而可得，由方程有两个不相等的正数根，（）可得，由方程得，且，由此分析整理即可得到答案；

（3）求出函数的导数，得到的单调性，求出的最小值，通过构造函数结合零点存在性定理判断函数的零点即可.

（1）依题意得，，，

∴ ．

令，得；令，得．

则函数在上单调递减，在上单调递增．

（2）由题意知：．

则，

令，得，

故方程有两个不相等的正数根，（），

则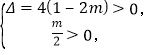 解得．

由方程得，且．

由，得．

，．

，即函数是上的增函数，

所以，故的取值范围是．

（3）依题意得，，，

∴ ．

令，得，∴ ，∵，

∴函数在上单调递减，在上单调递增，

∴．

令（），则，

∴，

∴，即．

∵，∴，

又∵，

∴，

根据零点存在性定理知函数在和各有一个零点．