题目内容
【题目】已知函数f(x)满足![]() ,当x∈[0,1]时,f(x)=x,若在区间(-1,1]上方程f(x)-mx-m=0有两个不同的实根,则实数m的取值范围是()
,当x∈[0,1]时,f(x)=x,若在区间(-1,1]上方程f(x)-mx-m=0有两个不同的实根,则实数m的取值范围是()
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
【答案】D
【解析】分析:设x∈(﹣1,0),则(x+1)∈(0,1),由于当x∈[0,1]时,f(x)=x,可得f(x+1)
=x+1.利用f(x)+1=![]() ,可得f(x)=
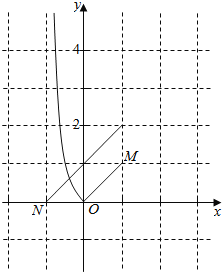
,可得f(x)=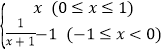 ,方程f(x)﹣mx﹣x=0,化为f(x)=mx+m,画出图象y=f(x),y=m(x+1),M(1,1),N(﹣1,0),可得kMN=
,方程f(x)﹣mx﹣x=0,化为f(x)=mx+m,画出图象y=f(x),y=m(x+1),M(1,1),N(﹣1,0),可得kMN=![]() .即可得出.
.即可得出.
详解:设x∈(﹣1,0),则(x+1)∈(0,1),
∵当x∈[0,1]时,f(x)=x,
∴f(x+1)=x+1.
∵f(x)+1=![]() ,可得f(x)=
,可得f(x)=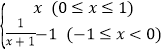 ,
,
方程f(x)﹣mx﹣x=0,化为f(x)=mx+m,
画出图象y=f(x),y=m(x+1),M(1,1),N(﹣1,0),
可得kMN=![]() .
.
∵在区间(﹣1,1]上方程f(x)﹣mx﹣x=0有两个不同的实根,
∴![]() ,
,
故答案为:D

练习册系列答案
 能力评价系列答案
能力评价系列答案 唐印文化课时测评系列答案
唐印文化课时测评系列答案 导学与测试系列答案
导学与测试系列答案
相关题目
【题目】为调查人们在购物时的支付习惯,某超市对随机抽取的600名顾客的支付方式进行了统计,数据如下表所示:
支付方式 | 微信 | 支付宝 | 购物卡 | 现金 |
人数 | 200 | 150 | 150 | 100 |
现有甲、乙、丙三人将进入该超市购物,各人支付方式相互独立,假设以频率近似代替概率.
(1)求三人中使用微信支付的人数多于现金支付人数的概率;
(2)记![]() 为三人中使用支付宝支付的人数,求
为三人中使用支付宝支付的人数,求![]() 的分布列及数学期望.
的分布列及数学期望.

