Question

【题目】（本小题满分16分）已知为实数，函数，函数．

（1）当时，令，求函数的极值；

（2）当时，令，是否存在实数，使得对于函数定义域中的任意实数，均存在实数，有成立，若存在，求出实数的取值集合；若不存在，请说明理由．

Answer 1

【答案】（1）的极小值为，无极大值．（2）

【解析】

试题分析：（1）当时，，定义域为，由得．列表分析得的极小值为，无极大值．（2）恒成立问题及存在问题，一般利用最值进行转化：在上恒成立．由于不易求，因此再进行转化：当时， 可化为，令，问题转化为：对任意恒成立；同理当时，可化为，令，问题转化为：对任意的恒成立；以下根据导函数零点情况进行讨论即可.

试题解析：（1），

，令，得． 1分

列表：

x
		0	+
	↘	极小值	↗

所以的极小值为，无极大值． 4分

（2）当时，假设存在实数满足条件，则在上恒成立． 5分

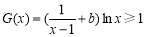1）当时， 可化为，

令，问题转化为：对任意恒成立；（*）

则，，．

令，则．

①时，因为，

故，所以函数在时单调递减，，

即，从而函数在时单调递增，故，所以（*）

成立，满足题意； 7分

②当时，，

因为，所以，记，则当时，，

故，所以函数在时单调递增，，

即，从而函数在时单调递减，所以，此时（*）不成立；

所以当，恒成立时，； 9分

2）当时，可化为，

令，问题转化为：对任意的恒成立；（**）

则，，．

令，则．

①时，，

故，所以函数在时单调递增，，

即，从而函数在时单调递增，所以，此时（**）成立；11分

②当时，

ⅰ）若，必有，故函数在上单调递减，所以，即，从而函数在时单调递减，所以，此时（**）不成立； 13分

ⅱ）若，则，所以当时，

，

故函数在上单调递减，，即，所以函数在时单调递减，所以，此时（**）不成立；

所以当，恒成立时，； 15分

综上所述，当，恒成立时， ，从而实数的取值集合为． 16分