题目内容
(本小题满分12分)设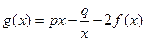
，其中
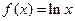，且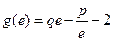
（
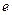为自然对数的底）
（1）求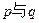
的关系；
（2）
在其定义域内的单调函数，求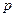
的取值范围；
（3）求证：（i）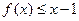
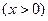
（ii）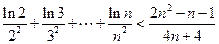
（
）。
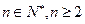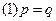
（2）
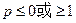
（3）证明略
解析
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
天天向上一本好卷系列答案小学生10分钟应用题系列答案题目内容
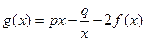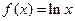(本小题满分12分)设，其中，且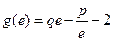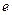（为自然对数的底）
（1）求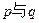的关系；
（2）在其定义域内的单调函数，求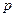的取值范围；
（3）求证：（i）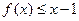
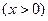
（ii） （）。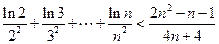
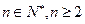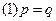
（2）
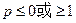
（3）证明略
解析
天天向上一本好卷系列答案小学生10分钟应用题系列答案
，存在实数
满足下列条件：
；②
；③
；
的定义域为R，对任意
，均有
，且对任意
都有
。
。
上的值域；
满足
，且对于任意的
，
.
对任意的
恒成立，求实数
的取值范围.
的函数
同时满足以下三个条件：
，总有
；②
；③若
且
，则有
成立，则称
的值；
在区间
，求证:
.
是定义在
上的奇函数,并且在
上是减函数．是否存在实数
使
恒成
立?若存在,求出实数
的一个根在-2与-1之间，另一个根在1与2之间，试求点
的轨迹及
的范围.