题目内容
19.已知点A(-1.0),B(1,0),若圆 (x-2)2+y2=r2上存在点P.使得∠APB=90°,则实数r的取值范围为( )| A. | (1,3) | B. | [1,3] | C. | (1,2] | D. | [2,3] |
分析 由题意可得两圆相交,而以AB为直径的圆的方程为x2+y2=1,圆心距为2,由两圆相交的性质可得|r-1|<2<|r+1|,由此求得r的范围.
解答 解:根据直径对的圆周角为90°,结合题意可得以AB为直径的圆和圆 (x-2)2+y2=r2有交点,
检验两圆相切时不满足条件,故两圆相交.
而以AB为直径的圆的方程为x2+y2=1,圆心距为2,
故|r-1|<2<|r+1|,求得1<r<3,
故选:A.
点评 本题主要考查直线和圆的位置关系,两圆相交的性质,体现了转化的数学思想,属于基础题.

练习册系列答案
 精英口算卡系列答案
精英口算卡系列答案 应用题点拨系列答案
应用题点拨系列答案
相关题目
14.已知 (1-2i)z=5(i为虚数单位),则复数z在复平面内对应的点所在象限为( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
8.已知过双曲线C:$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的中心的直线交双曲线于点A,B,在双曲线C上任取与点A,B不重合的点P,记直线PA,PB,AB的斜率分别为k1,k2,k,若k1k2>k恒成立,则离心率e的取值范围为( )
| A. | 1<e<$\sqrt{2}$ | B. | 1<e≤$\sqrt{2}$ | C. | e>$\sqrt{2}$ | D. | e≥$\sqrt{2}$ |
12.已知角α的终边在函数y=-|x|的图象上,则cosα的值为( )
| A. | $\frac{\sqrt{2}}{2}$ | B. | -$\frac{\sqrt{2}}{2}$ | C. | $±\frac{\sqrt{2}}{2}$ | D. | $\frac{1}{2}$ |
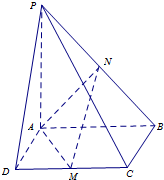 如图4,已知四棱锥P-ABCD,底面ABCD是正方形,PA⊥面ABCD,点M是CD的中点,点N是PB的中点,连接AM,AN,MN.
如图4,已知四棱锥P-ABCD,底面ABCD是正方形,PA⊥面ABCD,点M是CD的中点,点N是PB的中点,连接AM,AN,MN.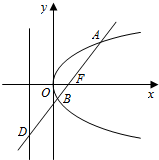 已知F为抛物线y2=4x的焦点,过点F引一条直线与抛物线交于A、B两点,与抛物线准线交于D点.
已知F为抛物线y2=4x的焦点,过点F引一条直线与抛物线交于A、B两点,与抛物线准线交于D点.