题目内容
【题目】已知函数![]() ,
,![]() 为
为![]() 的导函数.
的导函数.
(Ⅰ)当![]() 时,
时,
(i)求曲线![]() 在点
在点![]() 处的切线方程;
处的切线方程;
(ii)求函数![]() 的单调区间和极值;
的单调区间和极值;
(Ⅱ)当![]() 时,求证:对任意的
时,求证:对任意的![]() ,且
,且![]() ,有
,有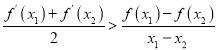 .
.
【答案】(Ⅰ)(i)![]() ;(ii)
;(ii)![]() 的极小值为
的极小值为![]() ,无极大值;(Ⅱ)证明见解析.
,无极大值;(Ⅱ)证明见解析.
【解析】
(Ⅰ) (i)首先求得导函数的解析式,然后结合导数的几何意义求解切线方程即可;
(ii)首先求得![]() 的解析式,然后利用导函数与原函数的关系讨论函数的单调性和函数的极值即可;
的解析式,然后利用导函数与原函数的关系讨论函数的单调性和函数的极值即可;
(Ⅱ)首先确定导函数的解析式,然后令![]() ,将原问题转化为与
,将原问题转化为与![]() 有关的函数,然后构造新函数,利用新函数的性质即可证得题中的结论.
有关的函数,然后构造新函数,利用新函数的性质即可证得题中的结论.
(Ⅰ) (i) 当k=6时,![]() ,
,![]() .可得
.可得![]() ,
,![]() ,
,
所以曲线![]() 在点
在点![]() 处的切线方程为
处的切线方程为![]() ,即
,即![]() .
.
(ii) 依题意,![]() .
.
从而可得![]() ,
,
整理可得:![]() ,
,
令![]() ,解得
,解得![]() .
.
当x变化时,![]() 的变化情况如下表:
的变化情况如下表:
|
|
|
|
|
|
|
|
| 单调递减 | 极小值 | 单调递增 |
所以,函数g(x)的单调递减区间为(0,1),单调递增区间为(1,+∞);
g(x)的极小值为g(1)=1,无极大值.
(Ⅱ)证明:由![]() ,得
,得![]() .
.
对任意的![]() ,且
,且![]() ,令
,令![]() ,则
,则
![]()
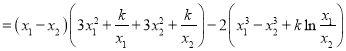
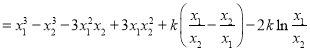
![]() . ①
. ①
令![]() .
.
当x>1时,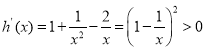 ,
,
由此可得![]() 在
在![]() 单调递增,所以当t>1时,
单调递增,所以当t>1时,![]() ,即
,即![]() .
.
因为![]() ,
,![]() ,
,![]() ,
,
所以![]()
![]() . ②
. ②
由(Ⅰ)(ii)可知,当![]() 时,
时,![]() ,即
,即![]() ,
,
故![]() ③
③
由①②③可得![]() .
.
所以,当![]() 时,任意的
时,任意的![]() ,且
,且![]() ,有
,有
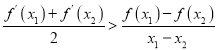 .
.

练习册系列答案
相关题目
【题目】质量是企业的生命线,某企业在一个批次产品中随机抽检![]() 件,并按质量指标值进行统计分析,得到表格如表:
件,并按质量指标值进行统计分析,得到表格如表:
质量指标值 | 等级 | 频数 | 频率 |
| 三等品 | 10 | 0.1 |
| 二等品 | 30 |
|
| 一等品 |
| 0.4 |
| 特等品 | 20 | 0.2 |
合计 |
| 1 | |
(1)求![]() ,
,![]() ,
,![]() ;
;
(2)从质量指标值在![]() 的产品中,按照等级分层抽样抽取6件,再从这6件中随机抽取2件,求至少有1件特等品被抽到的概率.
的产品中,按照等级分层抽样抽取6件,再从这6件中随机抽取2件,求至少有1件特等品被抽到的概率.
