Question

【题目】在四棱锥中，，.

(Ⅰ)若点为的中点，求证：∥平面；

(Ⅱ)当平面平面时，求二面角的余弦值.

Answer 1

【答案】（1）见解析； （2）.

【解析】

(I)结合平面与平面平行判定,得到平面BEM平行平面PAD,结合平面与平面性质,证明结论.(II)建立空间坐标系,分别计算平面PCD和平面PDB的法向量,结合向量数量积公式,计算余弦值,即可.

(Ⅰ)取的中点为，连结，.

由已知得，为等边三角形，.

∵，，

∴，

∴，∴.

又∵平面，平面，

∴∥平面.

∵为的中点，为的中点，∴∥.

又∵平面，平面，

∴∥平面.

∵，∴平面∥平面.

∵平面，∴∥平面.

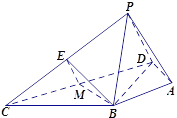
(Ⅱ)连结，交于点，连结，由对称性知，为的中点，且，.

∵平面平面，，

∴平面，，.

以为坐标原点，的方向为轴正方向，建立空间直角坐标系.

则(0，，0)，(3，0，0)，(0，0，1).

易知平面的一个法向量为.

设平面的法向量为，

则，，∴，

∵，，∴.

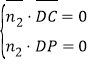令，得，∴，

∴.

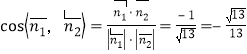设二面角的大小为，则.