题目内容
如图，AB为半圆的直径，P为半圆上一点，|AB|=10，∠PAB=a，且sina=
，建立适当的坐标系．
（1）求A、B为焦点且过P点的椭圆的标准方程．
（2）动圆M过点A，且与以B为圆心，以2
为半径的圆相外切，求动圆圆心M的轨迹方程．
| 4 |
| 5 |
（1）求A、B为焦点且过P点的椭圆的标准方程．
（2）动圆M过点A，且与以B为圆心，以2
| 5 |
（1）以直线AB为x轴，线段AB的垂直平分线为y轴，建立直角坐标系．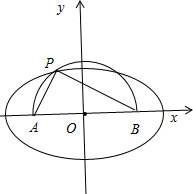
∵AB为半圆的直径，P为半圆上一点，∴∠APB=90°．
在Rt△APB中，|PB|=|AB|sinα=10×
=8，∴|AP|=6．
∴|PA|+|PB|=6+8=14=2a，解得a=7，
∵2c=10，∴c=5，
∴b2=a2-c2=24．
∴椭圆的标准方程为：
+
=1．
（2）由题意可得：|MB|-|MA|=2
＜10=|AB|，
故动圆圆心M的轨迹在双曲线的左支上，
∵2c′=10，2a′=2
，∴c′=5，a′=
，(b′)2=52-(
)2=20．
其方程为
-
=1(x≤-
)．
∵AB为半圆的直径，P为半圆上一点，∴∠APB=90°．
在Rt△APB中，|PB|=|AB|sinα=10×
| 4 |
| 5 |
∴|PA|+|PB|=6+8=14=2a，解得a=7，
∵2c=10，∴c=5，
∴b2=a2-c2=24．
∴椭圆的标准方程为：
| x2 |
| 49 |
| y2 |
| 24 |
（2）由题意可得：|MB|-|MA|=2
| 5 |
故动圆圆心M的轨迹在双曲线的左支上，
∵2c′=10，2a′=2
| 5 |
| 5 |
| 5 |
其方程为
| x2 |
| 5 |
| y2 |
| 20 |
| 5 |
练习册系列答案
口算题天天练系列答案
相关题目
，