题目内容
18.已知函数f(x)=|x2-a|在区间[-1,1]上的最大值为M(a),则M(a)min=$\frac{1}{2}$.分析 由题意可得函数f(x)为偶函数,因此讨论M(a)的值域只需在x∈[0,1]这一范围内进行,结合二次函数的单调性及a的正负及$\sqrt{a}$与1的大小分类讨论求解M(a).
解答 解:由题意可得函数f(x)为偶函数,因此讨论M(a)的值域只需在x∈[0,1]这一范围内进行;
①当a≤0时,f(x)=x2-a,函数f(x)在[0,1]单调递增,M(a)=f(1)=1-a≥1.
②当 1>a>0时,函数f(x)在[0,$\sqrt{a}$]上单调递减,在[$\sqrt{a}$,1]上单调递增,
所以f(x)在[0,$\sqrt{a}$]内的最大值为M(a)=f(0)=a,
而f(x)在[$\sqrt{a}$,1]上的最大值为M(a)=f(1)=1-a.
由f(1)>f(0)得1-a>a,即0<a<$\frac{1}{2}$.
故当a∈(0,$\frac{1}{2}$)时,M(a)=f(1)=1-a>$\frac{1}{2}$,
同理,当a∈[$\frac{1}{2}$,1)时,M(a)=f(0)=a≥$\frac{1}{2}$.
③当a≥1时,函数在[0,1]上为减函数,所以M(a)=f(0)=a≥1.
综上,M(a)=1-a,(当a<$\frac{1}{2}$时); M(a)=a,(当a≥$\frac{1}{2}$时).
所以M(a)在[0,$\frac{1}{2}$]上为减函数,且在[$\frac{1}{2}$,1]为增函数,易得M(a)的最小值为M($\frac{1}{2}$)=$\frac{1}{2}$.
故答案为:$\frac{1}{2}$.
点评 本题主要考查了偶函数的性质的应用,其实由分析可得M(a)=f(0)或f(1),所以可直接通过比较f(0)与f(1)的大小得出M(a)的解析式从而求解.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案| A. | 3+sinx | B. | 3-sinx | C. | 3-cosx | D. | 3+cosx |

| A. | 18 | B. | 32 | C. | 50 | D. | 72 |
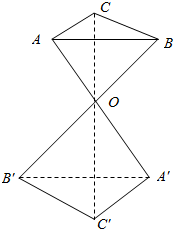 如图,△ABC和△A′B′C′的对应顶点的连线AA′,BB′,CC′交于同一点O,且$\frac{AO}{OA′}=\frac{BO}{OB′}=\frac{CO}{OC′}=\frac{2}{3}$.
如图,△ABC和△A′B′C′的对应顶点的连线AA′,BB′,CC′交于同一点O,且$\frac{AO}{OA′}=\frac{BO}{OB′}=\frac{CO}{OC′}=\frac{2}{3}$.