题目内容
6.若${∫}_{1}^{2}(x-a)dx$=${∫}_{0}^{\frac{3π}{4}}$cos2xdx,则a等于$\frac{4}{3}$.分析 分别根据定积分的计算法则求出,得到关于a的方程,解得即可.
解答 解:${∫}_{1}^{2}(x-a)dx$=($\frac{1}{2}$x2-ax)|${\;}_{1}^{2}$=2-2a-$\frac{1}{2}$+a=$\frac{3}{2}$-$\frac{3}{2}$a,
${∫}_{0}^{\frac{3π}{4}}$cos2xdx=$\frac{1}{2}$sin2x|${\;}_{0}^{\frac{3π}{4}}$=$\frac{1}{2}$sin$\frac{3π}{2}$=-$\frac{1}{2}$,
∴$\frac{3}{2}$-$\frac{3}{2}$a=-$\frac{1}{2}$,
∴a=$\frac{4}{3}$,
故答案为:$\frac{4}{3}$.
点评 本题考查了定积分的计算,关键求出原函数,属于基础题.

练习册系列答案
 互动课堂系列答案
互动课堂系列答案 激活思维智能训练课时导学练系列答案
激活思维智能训练课时导学练系列答案
相关题目
15.下列对应关系,不是数集M到数集N上的函数是( )
| A. | 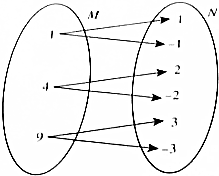 | B. | 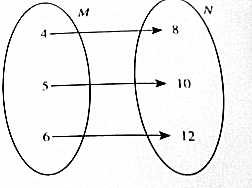 | ||
| C. | 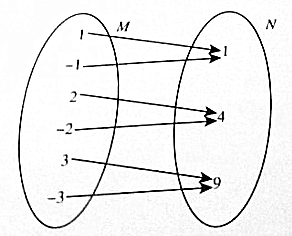 | D. | 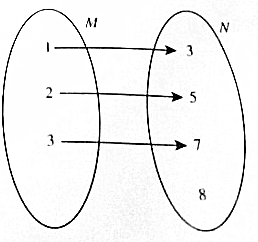 |