题目内容
4.已知函数f(x)=cos(2x-$\frac{π}{6}$).(1)求函数f(x)的单调递增区间;
(2)若x∈(-$\frac{π}{12}$,$\frac{π}{3}$),求f(x)的取值范围.
分析 (1)由条件利用余弦函数的单调性求得函数f(x)的单调递增区间.
(2)由x∈(-$\frac{π}{12}$,$\frac{π}{3}$),利用余弦函数定义域和值域,求得f(x)的取值范围.
解答 解:(1)对于函数f(x)=cos(2x-$\frac{π}{6}$),令2kπ-π≤2x-$\frac{π}{6}$≤2kπ,k∈z,
求得kπ-$\frac{5π}{12}$≤x≤kπ+$\frac{π}{12}$,可得函数f(x)的单调递增区间为[kπ-$\frac{5π}{12}$,kπ+$\frac{π}{12}$],k∈z.
(2)若x∈(-$\frac{π}{12}$,$\frac{π}{3}$),则2x-$\frac{π}{6}$∈(-$\frac{π}{3}$,$\frac{π}{2}$),
∴cos(2x-$\frac{π}{6}$)∈(0,1],
故f(x)∈(0,1].
点评 本题主要考查余弦函数的单调性、定义域和值域,属于基础题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
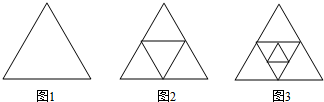
18.如图1是一个边长为1的正三角形,分别连接这个三角形三边中点,将在三角剖分成4个三角开(如图2),再分别连接图2中一个小三角形三边的中点,又可将原三角形剖分成7个三角形(如图3),…,依此类推,设第n个图中原三角形被剖分成an个三角形,则第4个图中最小三角形的边长为( );a100=( )

| A. | $\frac{1}{6}$,300 | B. | $\frac{1}{8}$,300 | C. | $\frac{1}{6}$,298 | D. | $\frac{1}{8}$,298 |
19.若数列{an}的前n项和Sn=n2-2n+3,则此数列的前3项依次为( )
| A. | -1,1,3 | B. | 2,3,6 | C. | 6,1,3 | D. | 2,1,3 |
16.为了解七班学生喜爱打篮球是否与性别有关,对本班50人进行了问卷调查得到了如下的列联表:已知在全部50人中随机抽取1人抽到喜爱打篮球的学生的概率为$\frac{3}{5}$.
(1)请将上面的列联表补充完整(不用写计算过程);
(2)能否在犯错误的概率不超过0.005的前提下认为喜爱打篮球与性别有关?说明你的理由.
| 喜爱打篮球 | 不喜爱打篮球 | 合计 | |
| 男生 | 5 | ||
| 女生 | 10 | ||
| 合计 | 50 |
(2)能否在犯错误的概率不超过0.005的前提下认为喜爱打篮球与性别有关?说明你的理由.
13.已知ω>0,函数f(x)=sinωx在区间[-$\frac{π}{4}$,$\frac{π}{4}$]上恰有9个零点,那么ω的取值范围为( )
| A. | [16,20) | B. | (16,20] | C. | (16,24) | D. | [16,24] |
 如图,已知正方形ABCD的边长为6,点E,F分别在边AB,AD上,AE=AF=4,现将△AEF沿线段EF折起到△A′EF位置,使得A′C=2$\sqrt{6}$.
如图,已知正方形ABCD的边长为6,点E,F分别在边AB,AD上,AE=AF=4,现将△AEF沿线段EF折起到△A′EF位置,使得A′C=2$\sqrt{6}$.