题目内容
【题目】选修4-4:坐标系与参数方程
已知曲线C的极坐标方程为ρ﹣4cosθ+3ρsin2θ=0,以极点为原点,极轴为x轴的正半轴建立平面直角坐标系,直线l过点M(1,0),倾斜角为![]() .
.
(Ⅰ)求曲线C的直角坐标方程与直线l的参数方程;
(Ⅱ)若曲线C经过伸缩变换![]() 后得到曲线C′,且直线l与曲线C′交于A,B两点,求|MA|+|MB|.
后得到曲线C′,且直线l与曲线C′交于A,B两点,求|MA|+|MB|.
【答案】(1)(x﹣2)2+4y2=4,  ,(t为参数);(2)
,(t为参数);(2)![]() .
.
【解析】试题分析:
(Ⅰ)极坐标方程化简直角坐标方程可得曲线C的直角坐标方程为(x﹣2)2+4y2=4,利用点的坐标和倾斜角可得直线的参数方程为 ,(t为参数);
,(t为参数);
(Ⅱ)利用题意求得伸缩变换之后的方程,然后利用弦长公式可得弦长为![]() .
.
试题解析:
(Ⅰ)∵曲线C的极坐标方程为ρ﹣4cosθ+3ρsin2θ=0,∴ρ2﹣4ρcosθ+3ρ2sin2θ=0,
∴曲线C的直角坐标方程为x2+y2﹣4x+3y2=0,整理,得(x﹣2)2+4y2=4,
∵直线l过点M(1,0),倾斜角为![]() ,
,
∴直线l的参数方程为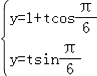 ,即
,即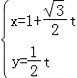 ,(t是参数).
,(t是参数).
(Ⅱ)∵曲线C经过伸缩变换![]() 后得到曲线C′,
后得到曲线C′,
∴曲线C′为:(x﹣2)2+y2=4,
把直线l的参数方程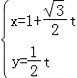 ,(t是参数)代入曲线C′:(x﹣2)2+y2=4,
,(t是参数)代入曲线C′:(x﹣2)2+y2=4,
得:![]() ,
,
设A,B对应的参数分别为t1,t2,则t1+t2=![]() ,t1t2=﹣3,
,t1t2=﹣3,
|MA|+|MB|=|t1|+|t2|=|t1﹣t2|=![]() =
=![]() =
=![]() .
.

 补充习题江苏系列答案
补充习题江苏系列答案 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案【题目】目前,学案导学模式已经成为教学中不可或缺的一部分,为了了解学案的合理使用是否对学生的期末复习有着重要的影响,我校随机抽取100名学生,对学习成绩和学案使用程度进行了调查,统计数据如表所示:
善于使用学案 | 不善于使用学案 | 总计 | |
学习成绩优秀 | 40 | ||
学习成绩一般 | 30 | ||
总计 | 100 |
参考公式:![]() ,其中
,其中![]() .
.
参考数据:
| 0.050 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10.828 |
已知随机抽查这100名学生中的一名学生,抽到善于使用学案的学生概率是0.6.
(1)请将上表补充完整(不用写计算过程);
(2)试运用独立性检验的思想方法分析:有多大的把握认为学生的学习成绩与对待学案的使用态度有关?
(3)若从学习成绩优秀的同学中随机抽取10人继续调查,采用何种方法较为合理,试说明理由.