题目内容
16.随机抽取一个年份,对西安市该年4月份的天气情况进行统计,结果如下:(Ⅰ)在4月份任取一天,估计西安市在该天不下雨的概率;
(Ⅱ)西安市某学校拟从4月份的一个晴天开始举行连续2天的运动会,估计运动会期间不下雨的概率.
| 日期 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 |
| 天气 | 晴 | 雨 | 阴 | 阴 | 阴 | 雨 | 阴 | 晴 | 晴 | 晴 | 阴 | 晴 | 晴 | 晴 | 晴 |
| 日期 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 |
| 天气 | 晴 | 阴 | 雨 | 阴 | 阴 | 晴 | 阴 | 晴 | 晴 | 晴 | 阴 | 晴 | 晴 | 晴 | 雨 |
分析 (Ⅰ)在4月份任取一天,不下雨的天数是26,即可估计西安市在该天不下雨的概率;
(Ⅱ)求得4月份中,前一天为晴天的互邻日期对有16个,其中后一天不下雨的有14个,可得晴天的次日不下雨的概率,即可得出结论.
解答 解:(Ⅰ)在4月份任取一天,不下雨的天数是26,以频率估计概率,估计西安市在该天不下雨的概率为$\frac{13}{15}$;
(Ⅱ)称相邻的两个日期为“互邻日期对”,由题意,4月份中,前一天为晴天的互邻日期对有16个,其中后一天不下雨的有14个,所以晴天的次日不下雨的概率为$\frac{7}{8}$,
从而估计运动会期间不下雨的概率为$\frac{7}{8}$.
点评 本题考查概率的应用,考查学生的计算能力,确定基本事件的个数是关键.

练习册系列答案
相关题目
1.下列函数为奇函数的是( )
| A. | y=$\sqrt{x}$ | B. | y=ex | C. | y=cosx | D. | y=ex-e-x |
8.变量x,y满足约束条件$\left\{\begin{array}{l}{x+y≥0}\\{x-2y+2≥0}\\{mx-y≤0}\end{array}\right.$,若z=2x-y的最大值为2,则实数m等于( )
| A. | -2 | B. | -1 | C. | 1 | D. | 2 |
5.阅读如图所示的程序框图,运行相应的程序,则输出的结果为( )
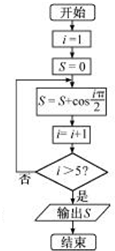

| A. | 2 | B. | 1 | C. | 0 | D. | -1 |
 如图,已知四棱台ABCD-A1B1C1D1的上、下底面分别是边长为3和6的正方形,AA1=6,且AA1⊥底面ABCD,点P、Q分别在棱DD1、BC上.
如图,已知四棱台ABCD-A1B1C1D1的上、下底面分别是边长为3和6的正方形,AA1=6,且AA1⊥底面ABCD,点P、Q分别在棱DD1、BC上.
 如图,某港口一天6时到18时的水渠变化曲线近似满足函数y=3sin($\frac{π}{6}$x+φ)+k.据此函数可知,这段时间水深(单位:m)的最大值为8.
如图,某港口一天6时到18时的水渠变化曲线近似满足函数y=3sin($\frac{π}{6}$x+φ)+k.据此函数可知,这段时间水深(单位:m)的最大值为8.