题目内容
10.函数f(x)=sin(ωx+φ)(ω>0,|φ|≤$\frac{π}{3}$)的最小正周期是π,若其图象向右平移$\frac{π}{3}$个单位后得到的函数为奇函数,则函数f(x)( )| A. | 关于点($\frac{π}{12}$,0)对称 | B. | 关于点($\frac{5π}{12}$,0)对称 | ||
| C. | 关于直线x=$\frac{5π}{12}$对称 | D. | 关于直线x=$\frac{π}{12}$对称 |
分析 根据条件求出函数的解析式,结合三角函数的对称性进行求解即可.
解答 解:若f(x)=sin(ωx+φ)(ω>0,|φ|≤$\frac{π}{3}$)的最小正周期是π,
则T=$\frac{2π}{ω}=π$,解得ω=2,
即f(x)=sin(2x+φ),
若其图象向右平移$\frac{π}{3}$个单位后得到y=sin[2(x-$\frac{π}{3}$)+φ]=sin(2x+φ-$\frac{2π}{3}$),
若此时函数为奇函数,
则φ-$\frac{2π}{3}$=kπ,k∈Z,
解得φ=$\frac{2π}{3}$+kπ,k∈Z,
∵|φ|≤$\frac{π}{3}$,
∴当k=-1时,φ=-$\frac{π}{3}$,
即f(x)=sin(2x-$\frac{π}{3}$),
由2x-$\frac{π}{3}$=$\frac{π}{2}+kπ$,
得x=$\frac{5π}{12}$+$\frac{kπ}{2}$,
故当k=0时,函数的对称轴为x=$\frac{5π}{12}$,
故函数关于直线x=$\frac{5π}{12}$对称,
故选:C.
点评 本题主要考查三角函数解析式的求解,以及三角函数性质的应用,求出函数的解析式是解决本题的关键.

练习册系列答案
 智趣暑假温故知新系列答案
智趣暑假温故知新系列答案 英语小英雄天天默写系列答案
英语小英雄天天默写系列答案 暑假作业安徽少年儿童出版社系列答案
暑假作业安徽少年儿童出版社系列答案
相关题目
18.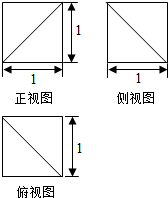 某几何体的三视图如图所示,则该几何体的体积是( )
某几何体的三视图如图所示,则该几何体的体积是( )
 某几何体的三视图如图所示,则该几何体的体积是( )
某几何体的三视图如图所示,则该几何体的体积是( )| A. | $\frac{5}{6}$ | B. | $\frac{2}{3}$ | C. | $\frac{1}{2}$ | D. | $\frac{1}{6}$ |
5.已知点O为双曲线C的对称中心,过点O的两条直线l1与l2的夹角为60°,直线l1与双曲线C相交于点A1,B1,直线l2与双曲线C相交于点A2,B2,若使|A1B1|=|A2B2|成立的直线l1与l2有且只有一对,则双曲线C离心率的取值范围是( )
| A. | ($\frac{2\sqrt{3}}{3}$,2] | B. | [$\frac{2\sqrt{3}}{3}$,2) | C. | ($\frac{2\sqrt{3}}{3}$,+∞) | D. | [$\frac{2\sqrt{3}}{3}$,+∞) |
15.已知圆C:(x-a)2+y2=1,直线l:x=1;则:“$\frac{1}{2}≤a≤\frac{3}{2}$”是“C上恰有不同四点到l的距离为$\frac{1}{2}$”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充分必要条件 | D. | 既不充分也不必要条件 |
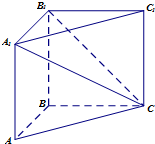 如图所示:在直三棱柱ABC-A1B1C1中,AB⊥BC,AB=BC=BB1,则平面A1B1C与平面ABC所成的二面角的大小为$\frac{π}{4}$.
如图所示:在直三棱柱ABC-A1B1C1中,AB⊥BC,AB=BC=BB1,则平面A1B1C与平面ABC所成的二面角的大小为$\frac{π}{4}$.