题目内容
5.已知点O为双曲线C的对称中心,过点O的两条直线l1与l2的夹角为60°,直线l1与双曲线C相交于点A1,B1,直线l2与双曲线C相交于点A2,B2,若使|A1B1|=|A2B2|成立的直线l1与l2有且只有一对,则双曲线C离心率的取值范围是( )| A. | ($\frac{2\sqrt{3}}{3}$,2] | B. | [$\frac{2\sqrt{3}}{3}$,2) | C. | ($\frac{2\sqrt{3}}{3}$,+∞) | D. | [$\frac{2\sqrt{3}}{3}$,+∞) |
分析 先设出双曲线的方程,并根据题意画出图象,根据对称性和条件判断出双曲线的渐近线斜率的范围,列出不等式并转化为关于离心率的不等式,再求解即可.
解答 解:不妨设双曲线的方程是$\frac{x^2}{a^2}-\frac{y^2}{b^2}$=1(a>0,b>0),
由|A1B1|=|A2B2|及双曲线的对称性知A1,A2,B1,B2关于x轴对称,如图,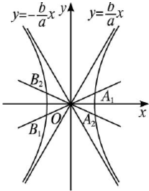
又∵满足条件的直线只有一对,
当直线与x轴夹角为30°时,双曲线的渐近线与x轴夹角大于30°,
双曲线与直线才能有交点A1,A2,B1,B2,
若双曲线的渐近线与x轴夹角等于30°,则无交点,
且不可能存在|A1B1|=|A2B2|,
当直线与x轴夹角为60°时,双曲线渐近线与x轴夹角小于60°,
双曲线与直线有一对交点A1,A2,B1,B2,
若双曲线的渐近线与x轴夹角等于60°,也满足题中有一对直线,
但是如果大于60°,则有两对直线.不符合题意,
∴tan30°<$\frac{b}{a}$≤tan60°,则$\frac{\sqrt{3}}{3}<\frac{b}{a}≤\sqrt{3}$,即$\frac{1}{3}<\frac{{b}^{2}}{{a}^{2}}≤3$,
∵b2=c2-a2,∴$\frac{1}{3}<\frac{{c}^{2}-{a}^{2}}{{a}^{2}}≤3$,则$\frac{1}{3}<{e}^{2}-1≤3$,
解得$\frac{4}{3}<{e}^{2}≤4$,即$\frac{2\sqrt{3}}{3}<e≤2$,
∴双曲线离心率的范围是($\frac{2\sqrt{3}}{3},2$],
故选:A.
点评 本题考查双曲线的简单性质以及应用,考查数形结合思想和分类讨论思想,属于中档题.

练习册系列答案
 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案
相关题目
10.函数f(x)=sin(ωx+φ)(ω>0,|φ|≤$\frac{π}{3}$)的最小正周期是π,若其图象向右平移$\frac{π}{3}$个单位后得到的函数为奇函数,则函数f(x)( )
| A. | 关于点($\frac{π}{12}$,0)对称 | B. | 关于点($\frac{5π}{12}$,0)对称 | ||
| C. | 关于直线x=$\frac{5π}{12}$对称 | D. | 关于直线x=$\frac{π}{12}$对称 |
10.某市工业部门计划对所辖中小型工业企业推行节能降耗技术改造,对所辖企业是否支持改造进行问卷调查,结果如表:
(Ⅰ)能否在犯错误的概率不超过0.025的前提下认为“是否支持节能降耗技术改造”与“企业规模”有关?
(Ⅱ)从上述320家支持节能降耗改造的中小企业中按分层抽样的方法抽出8家,然后从这8家中选出2家,求这2家中恰好中、小型企业各一家的概率
K2=$\frac{n(ad-bc)^{2}}{(a+b)(c+d)(b+d)}$
| 支持 | 不支持 | 合计 | |
| 中型企业 | 80 | 40 | 120 |
| 小型企业 | 240 | 200 | 440 |
| 合计 | 320 | 240 | 560 |
(Ⅱ)从上述320家支持节能降耗改造的中小企业中按分层抽样的方法抽出8家,然后从这8家中选出2家,求这2家中恰好中、小型企业各一家的概率
K2=$\frac{n(ad-bc)^{2}}{(a+b)(c+d)(b+d)}$
| P(K2≥k0) | 0.050 | 0.025 | 0.010 |
| K0 | 3.841 | 5.024 | 6.635 |