题目内容
5.已知函数f(x)=lg$\frac{kx-1}{x-1}$.(1)求f(x)的定义域;
(2)若f(x)在[2,+∞)上单调增,求k的取值范围.
分析 (1)根据对数函数的真数大于0,对k进行分类讨论,可得不同情况下函数的定义域;
(2)若f(x)在[2,+∞)上单调增,则t=$\frac{kx-1}{x-1}$为增函数,且当x=2时,$\frac{kx-1}{x-1}$>0,解得k的取值范围.
解答 解:(1)当k=0时,$\frac{kx-1}{x-1}$=$\frac{-1}{x-1}$>0得:x∈(-∞,1),即此时函数f(x)的定义域为(-∞,1),
当k<0时,解$\frac{kx-1}{x-1}$>0得:x∈($\frac{1}{k}$,1),即此时函数f(x)的定义域为($\frac{1}{k}$,1),
当0<k<1时,解$\frac{kx-1}{x-1}$>0得:x∈(-∞,1)∪($\frac{1}{k}$,+∞),即此时函数f(x)的定义域为(-∞,1)∪($\frac{1}{k}$,+∞),
当k=1时,解$\frac{kx-1}{x-1}$>0得:x∈(-∞,1)∪(1,+∞),即此时函数f(x)的定义域为(-∞,1)∪(1,+∞),
当k>1时,解$\frac{kx-1}{x-1}$>0得:x∈(-∞,$\frac{1}{k}$)∪(1,+∞),即此时函数f(x)的定义域为(-∞,$\frac{1}{k}$)∪(1,+∞),
(2)若f(x)在[2,+∞)上单调增,则t=$\frac{kx-1}{x-1}$=$\frac{k-1}{x-1}+k$为增函数,且当x=2时,$\frac{kx-1}{x-1}$>0,
即$\left\{\begin{array}{l}k-1<0\\ 2k-1>0\end{array}\right.$,
解得:k∈($\frac{1}{2}$,1).
点评 本题考查的知识点是对数函数的图象和性质,熟练掌握对数函数的图象和性质,是解答的关键.

| A. | $\frac{-1+2i}{3}$ | B. | $\frac{1+2i}{3}$ | C. | $\frac{1+2i}{5}$ | D. | $\frac{-1+2i}{5}$ |
| A. | f(1)<f(-2)<f(3) | B. | f(3)<f(1)<f(-2) | C. | f(一2)<f(1)<f(3) | D. | f(3)<f(-2)<f(1) |
| A. | 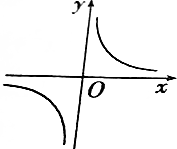 | B. | 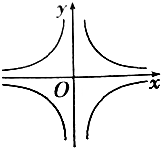 | ||
| C. | 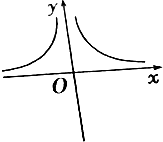 | D. | 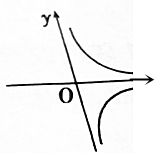 |
| A. | 3 | B. | 6 | C. | 9 | D. | 36 |
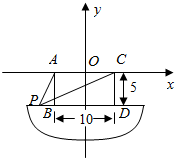 船上两根高5m的桅杆相距10m,一条30m长的绳子两端系在桅杆的顶上,并按如图所示的方式绷紧,假设绳子位于两根桅杆所在的平面内,求绳子与甲板接触点P到桅杆AB的距离.
船上两根高5m的桅杆相距10m,一条30m长的绳子两端系在桅杆的顶上,并按如图所示的方式绷紧,假设绳子位于两根桅杆所在的平面内,求绳子与甲板接触点P到桅杆AB的距离.