Question

3．抛物线y²=x的焦点为F，点P（x，y）为抛物线上的动点，又点A（-$\frac{1}{4}$，0）．则$\frac{|PF|}{|PA|}$的最小值$\frac{\sqrt{2}}{2}$．

Answer 1

分析 过点P作PM垂直于准线，M为垂足，则由抛物线的定义可得|PF|=|PM|，则$\frac{|PF|}{|PA|}$=$\frac{|PM|}{|PA|}$=sin∠PAM，故当PA和抛物线相切时，$\frac{|PF|}{|PA|}$最小．再利用直线的斜率公式、导数的几何意义求得切点的坐标，从而求得$\frac{|PF|}{|PA|}$最小值．

解答 解：由题意可得，焦点F（$\frac{1}{4}$，0），准线方程为x=-$\frac{1}{4}$．
过点P作PM垂直于准线，M为垂足，则由抛物线的定义可得|PF|=|PM|，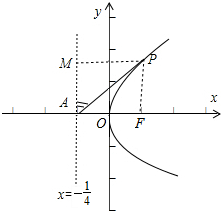

则$\frac{|PF|}{|PA|}$=$\frac{|PM|}{|PA|}$=sin∠PAM，其中∠PAM 为锐角．
故当∠PAM 最小时，$\frac{|PF|}{|PA|}$最小，
故当PA和抛物线相切时，$\frac{|PF|}{|PA|}$最小．
设切点P（a，$\sqrt{a}$），则PA的斜率为$\frac{\sqrt{a}}{a+\frac{1}{4}}$=$\frac{1}{2\sqrt{a}}$，
求得a=$\frac{1}{4}$，可得P（$\frac{1}{4}$，$\frac{1}{2}$），
∴|PM|=$\frac{1}{2}$，|PA|=$\frac{\sqrt{2}}{2}$，sin∠PAM=$\frac{|PM|}{|PA|}$=$\frac{\sqrt{2}}{2}$，
故答案为：$\frac{\sqrt{2}}{2}$．

点评 本题主要考查抛物线的定义、性质的简单应用，直线的斜率公式、导数的几何意义，属于中档题．