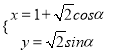题目内容
【题目】下列四个命题:(1)函数f(x)在[0,+∞)上是增函数,在(﹣∞,0)上也是增函数,所以f(x)在R上是增函数;(2)若函数f(x)=ax2+bx+2与x轴没有交点,则b2﹣8a<0,且a>0; (3)y=x2﹣2|x|﹣3的递增区间为[1,+∞);(4)函数y=lg10x和函数y=elnx表示相同函数.其中正确命题的个数是( )
A.3
B.2
C.1
D.0
【答案】D
【解析】解:对于(1),如函数f(x)=﹣ ![]() 在[0,+∞)上是增函数,在(﹣∞,0)上也是增函数,但不能说f(x)在R上是增函数,故错;对于(2),若函数f(x)=ax2+bx+2与x轴没有交点,则b2﹣8a<0,a>0或a<0都可以,还有a=b=0时也满足,故错;
在[0,+∞)上是增函数,在(﹣∞,0)上也是增函数,但不能说f(x)在R上是增函数,故错;对于(2),若函数f(x)=ax2+bx+2与x轴没有交点,则b2﹣8a<0,a>0或a<0都可以,还有a=b=0时也满足,故错;
对于 (3),∵y=x2﹣2|x|﹣3是偶函数其递增区间为[1,+∞),(﹣∞,﹣1],故错;
对于(4),函数y=lg10x (x∈R),函数y=elnx(x>0),定义与不同,故错.
故选:D.
【考点精析】认真审题,首先需要了解命题的真假判断与应用(两个命题互为逆否命题,它们有相同的真假性;两个命题为互逆命题或互否命题,它们的真假性没有关系).

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目