题目内容
已知数列 的相邻两项
的相邻两项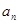 ,
,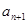 是关于
是关于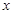 方程
方程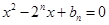 的两根,且
的两根,且 .
.
(1)求证:数列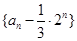 是等比数列;
是等比数列;
(2)求数列 的前
的前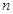 项和
项和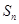 ;
;
(3)设函数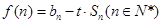 ,若
,若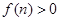 对任意的
对任意的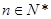 都成立,求实数
都成立,求实数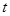 的取值范围.
的取值范围.
(1)见解析(2) (3)
(3)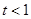
解析试题分析:(1)由一元二次方程根与系数的关系可得数列 的递推公式:
的递推公式: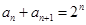 ,
,
设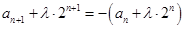 ,易求得:
,易求得: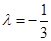 ,
, ,
,
并注意到: 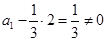 ,可知数列
,可知数列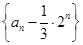 是公比为
是公比为 的等比数列.
的等比数列.
(2)由(1)的结果得数列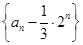 的通项公式
的通项公式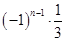 ,于是:
,于是: 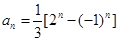 ,的拆项法,将数列
,的拆项法,将数列 的前
的前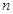 项和
项和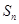 化为两个等比数列的前
化为两个等比数列的前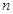 和.
和.
(3)由韦达定理: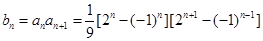 =
=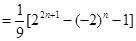
所以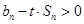 ,采用分离变量法求将求实数
,采用分离变量法求将求实数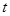 的取值范围问题,转变成求关于的函数的最值问题.
的取值范围问题,转变成求关于的函数的最值问题.
试题解析:(1)∵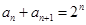 ,∴
,∴ ,
,
∵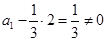 ,
,
∴ ,
,
∴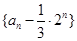 是首项为
是首项为 ,公比为
,公比为 的等比数列。
的等比数列。
且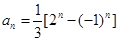 4分
4分
(2)由(1)得 =
=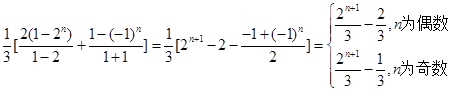 8分(注:未分奇偶写也得8分)
8分(注:未分奇偶写也得8分)
(3)∵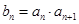 ,
,
∴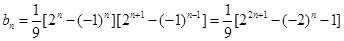 ,∴
,∴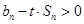 ,
,
∴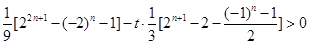 .
.
∴当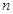 为奇数时,
为奇数时,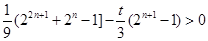 ,
,
∴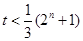 对任意的
对任意的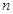 为奇数都成立,∴
为奇数都成立,∴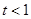 。 11分
。 11分
∴当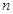 为偶数时,
为偶数时,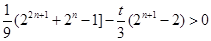 ,
,
∴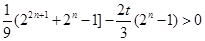 ,
,
∴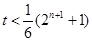 对任意的
对任意的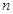 为偶数都成立,∴
为偶数都成立,∴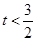 13分
13分
综上所述,实数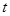 的取值范围为
的取值范围为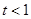 。 14分
。 14分
考点:1、一元二次方程根与系数的关系;2、等比数列的前 项和;3、等价转化的思想.
项和;3、等价转化的思想.

练习册系列答案
 口算能手系列答案
口算能手系列答案
相关题目
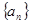 中
中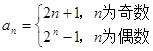 , 则
, 则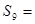 。
。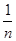 )+f(
)+f(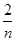 )+f(
)+f(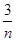 )+…+f(
)+…+f(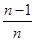 )+f(1).
)+f(1).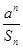 (a∈R)且bn<bn+1对所有正整数n恒成立,求a的取值范围.
(a∈R)且bn<bn+1对所有正整数n恒成立,求a的取值范围.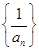 是公差为
是公差为 的等差数列,且
的等差数列,且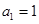 .
.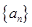 的通项公式;
的通项公式;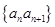 的前
的前 项和为
项和为 .
.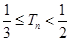 .
.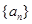 的前
的前 项和为
项和为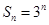 ,数列
,数列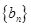 满足
满足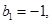
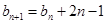 (
(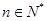 ).
).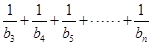 的值.
的值.
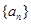 的前项和为
的前项和为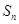 ,且满足
,且满足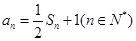 ;
;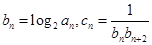 ,且
,且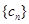 的前n项和为
的前n项和为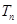 ,求使得
,求使得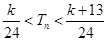 对
对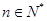 都成立的所有正整数k的值.
都成立的所有正整数k的值. 中,
中, ,其前
,其前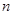 项和为
项和为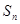 ,等比数列
,等比数列 的各项均为正数,
的各项均为正数,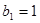 ,公比为
,公比为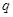 ,且
,且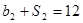 ,
, .
.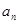 与
与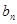 ;
;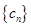 满足
满足 ,求
,求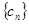 的前
的前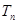 .
.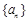 中,
中, ,
,
 且
且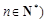 .
. ,
,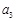 的值;
的值; 是等比数列,并求
是等比数列,并求 项和
项和 .
.