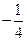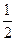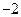题目内容
已知函数f(x)=alnx-x2,x=1是f(x)的一个极值点.
(1)求a的值;
(2)若方程f(x)+m=0在[
,e]内有两个不等实根,求m的取值范围(其中e为自然对数的底数);
(3)令g(x)=f(x)+3x,若g(x)的图象与x轴交于A(x1,0),B(x2,0)(其中x1<x2),求证:
<x2-x1<
.(参考数据:ln2≈0.7 e≈2.7)
(1)求a的值;
(2)若方程f(x)+m=0在[
| 1 |
| e |
(3)令g(x)=f(x)+3x,若g(x)的图象与x轴交于A(x1,0),B(x2,0)(其中x1<x2),求证:
| 5 |
| 2 |
| 7 |
| 2 |
(1)求导函数可得f′(x)=
-2x=-
(x>0)
∵x=1是f(x)的一个极值点.
∴f′(1)=0,可得a=2.
(2)f(x)=2lnx-x2,令h(x)=f(x)+m=2lnx-x2+m,
则h′(x)=
-2x=-
(x-1)(x+1),
令h′(x)=0,得x=1(x=-1舍去).
由于x∈[
,e],
则当x∈[
,1]时,h′(x)>0,∴h(x)是增函数;
当x∈[1,e]时,h′(x)<0,∴h(x)是减函数,
则方程h(x)=0在[
,e]内有两个不等实根的充要条件是:
即1<m≤2+
.
(3)若g(x)的图象与x轴交于A(x1,0),B(x2,0)(其中x1<x2),
则方程2lnx-x2+3x=0的解为x1,x2(其中x1<x2).
故函数y=2lnx与y=x2-3x的交点的横坐标为x1,x2,
作出两函数图象如图.如图所示,
由于2ln
=-2ln2≈-1.4,(
)2-3×
=-
=-1.25,所以
<x1<1,
同理得到
<x2<4,
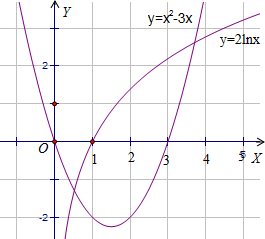
故-1<-x1<-
,所以
<x2-x1<
.
| a |
| x |
| 2x2-a |
| x |
∵x=1是f(x)的一个极值点.
∴f′(1)=0,可得a=2.
(2)f(x)=2lnx-x2,令h(x)=f(x)+m=2lnx-x2+m,
则h′(x)=
| 2 |
| x |
| 2 |
| x |
令h′(x)=0,得x=1(x=-1舍去).
由于x∈[
| 1 |
| e |
则当x∈[
| 1 |
| e |
当x∈[1,e]时,h′(x)<0,∴h(x)是减函数,
则方程h(x)=0在[
| 1 |
| e |
|
即1<m≤2+
| 1 |
| e2 |
(3)若g(x)的图象与x轴交于A(x1,0),B(x2,0)(其中x1<x2),
则方程2lnx-x2+3x=0的解为x1,x2(其中x1<x2).
故函数y=2lnx与y=x2-3x的交点的横坐标为x1,x2,
作出两函数图象如图.如图所示,
由于2ln
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 5 |
| 4 |
| 1 |
| 2 |
同理得到
| 7 |
| 2 |
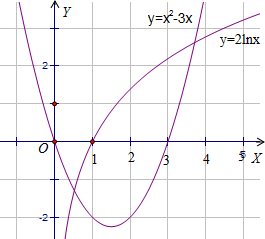
故-1<-x1<-
| 1 |
| 2 |
| 5 |
| 2 |
| 7 |
| 2 |

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
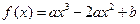 ,(
,(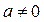 ).(Ⅰ)求出f(x)的极值点,并指出其是极大值点还是极小值点;(Ⅱ)若f(x)在区间
).(Ⅰ)求出f(x)的极值点,并指出其是极大值点还是极小值点;(Ⅱ)若f(x)在区间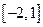 上最大值是5,最小值是-11,求
上最大值是5,最小值是-11,求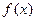 的解析式.
的解析式.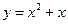 ,则在闭区间
,则在闭区间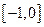 上的最小值是( )
上的最小值是( )