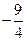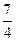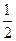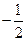题目内容
设a∈R,f(x)=x3-x2-x+a,曲线y=f(x)与x轴有且只有一个公共点,实数a的取值范围是______.
求一阶导数可得f'(x)=3x2-2x-1,
两个极值点分别在x=1、x=-
,
代入函数,得f(1)=a-1,f(-
)=a+
,
当a-1>0时,f(1)>0,得出a>1,
当a+
<0时,f(-
)<0,得出a<-
,
则曲线y=f(x)与x轴有且只有一个公共点,实数a的取值范围为:(-∞,-
)∪(1,+∞),
故答案为:(-∞,-
)∪(1,+∞).
两个极值点分别在x=1、x=-
| 1 |
| 3 |
代入函数,得f(1)=a-1,f(-
| 1 |
| 3 |
| 5 |
| 27 |
当a-1>0时,f(1)>0,得出a>1,
当a+
| 5 |
| 27 |
| 1 |
| 3 |
| 5 |
| 27 |
则曲线y=f(x)与x轴有且只有一个公共点,实数a的取值范围为:(-∞,-
| 5 |
| 27 |
故答案为:(-∞,-
| 5 |
| 27 |

练习册系列答案
 学练快车道快乐假期暑假作业新疆人民出版社系列答案
学练快车道快乐假期暑假作业新疆人民出版社系列答案 浙大优学小学年级衔接导与练浙江大学出版社系列答案
浙大优学小学年级衔接导与练浙江大学出版社系列答案 小学暑假作业东南大学出版社系列答案
小学暑假作业东南大学出版社系列答案 津桥教育暑假拔高衔接广东人民出版社系列答案
津桥教育暑假拔高衔接广东人民出版社系列答案 波波熊暑假作业江西人民出版社系列答案
波波熊暑假作业江西人民出版社系列答案
相关题目
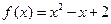 的极值是( )
的极值是( )