题目内容
方程x3-6x2+9x+1=0的实根个数是( )
| A.1 | B.2 | C.3 | D.4 |
设f(x)=x3-6x2+9x+1,
∴f′(x)=3x2-12x+9,
令f′(x)=0,解得x1=1或x=3,
当x<1时,f′(x)>0,则f(x)在(-∞,1)上单调递增,
当1<x<3时,f′(x)<0,则f(x)在(1,3)上单调递减,
当x>3时,f′(x)>0,则f(x)在(3,+∞)上单调递增,
∴当x=1时,函数f(x)取得极大值f(1)=5,
当x=3时,函数f(x)取得极小值f(3)=1,
∵f(1)>0,f(3)>0,
∴函数f(x)与x轴只有一个交点,
∴方程x3-6x2+9x+1=0的实根个数是1个.
故选A.
∴f′(x)=3x2-12x+9,
令f′(x)=0,解得x1=1或x=3,
当x<1时,f′(x)>0,则f(x)在(-∞,1)上单调递增,
当1<x<3时,f′(x)<0,则f(x)在(1,3)上单调递减,
当x>3时,f′(x)>0,则f(x)在(3,+∞)上单调递增,
∴当x=1时,函数f(x)取得极大值f(1)=5,
当x=3时,函数f(x)取得极小值f(3)=1,
∵f(1)>0,f(3)>0,
∴函数f(x)与x轴只有一个交点,
∴方程x3-6x2+9x+1=0的实根个数是1个.
故选A.

练习册系列答案
 期末金牌卷系列答案
期末金牌卷系列答案 轻松课堂标准练系列答案
轻松课堂标准练系列答案
相关题目
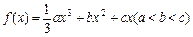 ,其图象在点
,其图象在点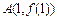 ,
,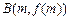 处的切线的斜率分别为
处的切线的斜率分别为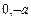
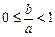 ;
; 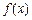 的递增区间为
的递增区间为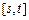 ,求|
,求|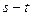 |的取值范围;
|的取值范围;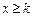 时(
时(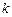 是与
是与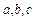 无关的常数),恒有
无关的常数),恒有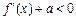 ,试求
,试求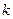 的最小值。
的最小值。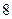 分为两个数,使其和为
分为两个数,使其和为