题目内容
【题目】下列四个命题,其中m,n,l为直线,α,β为平面
①mα,nα,m∥β,n∥βα∥β;
②设l是平面α内任意一条直线,且l∥βα∥β;
③若α∥β,mα,nβm∥n;
④若α∥β,mαm∥β.
其中正确的是( )
A.①②
B.②③
C.②④
D.①②④
【答案】C
【解析】解:在长方体ABCD﹣A1B1C1D1中,
①若平面AC是平面α,平面A1C1是平面β,
直线AD是直线m,A1B1是直线n,
显然满足mα,nα,m∥β,n∥β,但是α与β相交,不正确;
②若平面α内任意一条直线平行于平面β,则平面α的两条相交直线平行于平面β,满足面面平行的判定定理,所以α∥β;故正确
③若平面AC是平面α,平面BC1是平面β,
直线AD是直线m,点E,F分别是AB,CD的中点,则EF∥AD,EF是直线n,
显然满足α∥β,mα,nβ,但是m与n异面,不正确;
④由面面平行结合线面平行的定义可得m∥β,正确,
故选:C.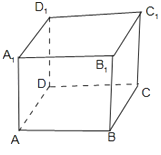
【考点精析】利用空间中直线与平面之间的位置关系对题目进行判断即可得到答案,需要熟知直线在平面内—有无数个公共点;直线与平面相交—有且只有一个公共点;直线在平面平行—没有公共点.

练习册系列答案
相关题目