题目内容
【题目】已知函数f(x)的定义域为R,且f(x)不为常值函数,有以下命题:
①函数g(x)=f(x)+f(﹣x)一定是偶函数;
②若对任意x∈R都有f(x)+f(2﹣x)=0,则f(x)是以2为周期的周期函数;
③若f(x)是奇函数,且对于任意x∈R,都有f(x)+f(2+x)=0,则f(x)的图象的对称轴方程为x=2n+1(n∈Z);
④对于任意的x1 , x2∈R,且x1≠x2 , 若![]() >0恒成立,则f(x)为R上的增函数,
>0恒成立,则f(x)为R上的增函数,
其中所有正确命题的序号是 .
【答案】①③④
【解析】解:∵g(﹣x)=f(﹣x)+f(x)=g(x),故函数g(x)=f(x)+f(﹣x)一定是偶函数,故①正确;
②若对任意x∈R都有f(x)+f(2﹣x)=0,则f(x)的图象关于点(1,0)对称,但不一定是周期函数,故错误;
③若f(x)是奇函数,且对于任意x∈R,都有f(x)+f(2+x)=0,则函数的周期为4,则f(x)的图象的对称轴方程为x=2n+1(n∈Z),故正确;
④对于任意的x1 , x2∈R,且x1≠x2 , 若![]() >0恒成立,则f(x)为R上的增函数,故正确,
>0恒成立,则f(x)为R上的增函数,故正确,
故答案为:①③④
根据函数奇偶性的定义,可判断①;根据已知分析函数的对称性,可判断②;根据已知分析出函数的周期性和对称性,可判断③;根据已知分析出函数的单调性,可判断④

 新卷王期末冲刺100分系列答案
新卷王期末冲刺100分系列答案 全能闯关100分系列答案
全能闯关100分系列答案【题目】网购是当前民众购物的新方式,某公司为改进营销方式,随机调查了100名市民,统计其周平均网购的次数,并整理得到如下的频数分布直方图.这100名市民中,年龄不超过40岁的有65人将所抽样本中周平均网购次数不小于4次的市民称为网购迷,且已知其中有5名市民的年龄超过40岁.
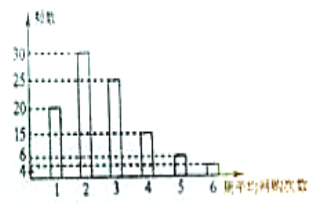
(1)根据已知条件完成下面的![]() 列联表,能否在犯错误的概率不超过0.10的前提下认为网购迷与年龄不超过40岁有关?
列联表,能否在犯错误的概率不超过0.10的前提下认为网购迷与年龄不超过40岁有关?
网购迷 | 非网购迷 | 合计 | |
年龄不超过40岁 | |||
年龄超过40岁 | |||
合计 |
(2)若从网购迷中任意选取2名,求其中年龄超过40岁的市民人数![]() 的分布列与期望.
的分布列与期望.
附: 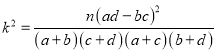 ;
;
| 0.15 | 0.10 | 0.05 | 0.01 |
| 2.072 | 2.706 | 3.841 | 6.635 |