题目内容
(本题满分12分)设函数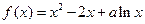 。
。
???(1)若函数 是定义域上的单调函数,求实数
是定义域上的单调函数,求实数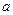 的取值范围;
的取值范围;
???(2)求函数 的极值点。
的极值点。
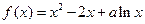 。
。???(1)若函数
 是定义域上的单调函数,求实数
是定义域上的单调函数,求实数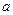 的取值范围;
的取值范围;???(2)求函数
 的极值点。
的极值点。1)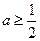 (2)
(2)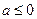 时,
时, 在
在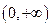 上有唯一的极小值点
上有唯一的极小值点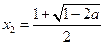 ;
;
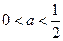 时,
时, 有一个极大值点
有一个极大值点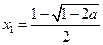 和一个极小值点
和一个极小值点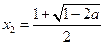 ;
;
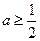 时,函数
时,函数 在
在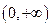 上无极值点。
上无极值点。
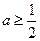 (2)
(2)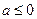 时,
时, 在
在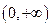 上有唯一的极小值点
上有唯一的极小值点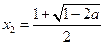 ;
;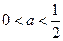 时,
时, 有一个极大值点
有一个极大值点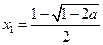 和一个极小值点
和一个极小值点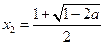 ;
;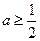 时,函数
时,函数 在
在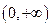 上无极值点。
上无极值点。1)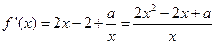 ,若函数
,若函数 是定义域上的单调函数,则只能
是定义域上的单调函数,则只能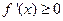 在
在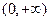 上恒成立,即
上恒成立,即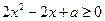 在
在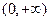 上恒成立恒成立,令
上恒成立恒成立,令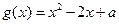 ,则函数
,则函数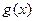 图象的对称轴方程是
图象的对称轴方程是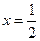 ,故只要
,故只要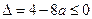 恒成立,即只要
恒成立,即只要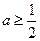 。(5分)
。(5分)
(2)有(1)知当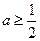 时,
时,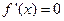 的点是导数不变号的点,
的点是导数不变号的点,
故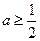 时,函数无极值点;
时,函数无极值点;
当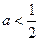 时,
时,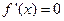 的根是
的根是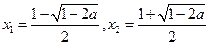 ,
,
若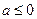 ,
,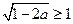 ,此时
,此时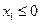 ,
,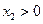 ,且在
,且在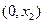 上
上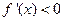 ,
,
在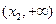 上
上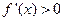 ,故函数
,故函数 有唯一的极小值点
有唯一的极小值点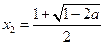 ;(7分)
;(7分)
当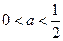 时,
时,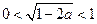 ,此时
,此时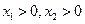 ,
,
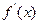 在
在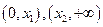 都大于
都大于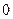 ,
,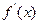 在
在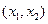 上小于
上小于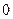 ,
,
此时 有一个极大值点
有一个极大值点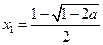 和一个极小值点
和一个极小值点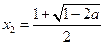 .(11分)
.(11分)
综上可知,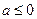 时,
时, 在
在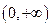 上有唯一的极小值点
上有唯一的极小值点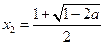 ;
;
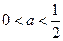 时,
时, 有一个极大值点
有一个极大值点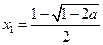 和一个极小值点
和一个极小值点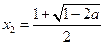 ;
;
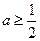 时,函数
时,函数 在
在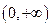 上无极值点。(12分)
上无极值点。(12分)
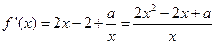 ,若函数
,若函数 是定义域上的单调函数,则只能
是定义域上的单调函数,则只能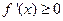 在
在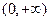 上恒成立,即
上恒成立,即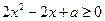 在
在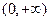 上恒成立恒成立,令
上恒成立恒成立,令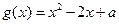 ,则函数
,则函数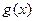 图象的对称轴方程是
图象的对称轴方程是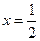 ,故只要
,故只要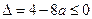 恒成立,即只要
恒成立,即只要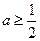 。(5分)
。(5分)(2)有(1)知当
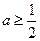 时,
时,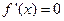 的点是导数不变号的点,
的点是导数不变号的点,故
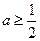 时,函数无极值点;
时,函数无极值点;当
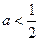 时,
时,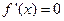 的根是
的根是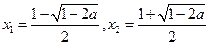 ,
,若
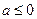 ,
,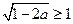 ,此时
,此时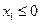 ,
,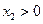 ,且在
,且在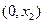 上
上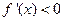 ,
,在
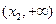 上
上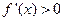 ,故函数
,故函数 有唯一的极小值点
有唯一的极小值点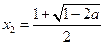 ;(7分)
;(7分)当
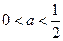 时,
时,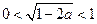 ,此时
,此时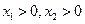 ,
,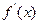 在
在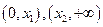 都大于
都大于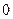 ,
,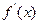 在
在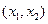 上小于
上小于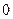 ,
,此时
 有一个极大值点
有一个极大值点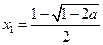 和一个极小值点
和一个极小值点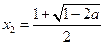 .(11分)
.(11分)综上可知,
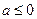 时,
时, 在
在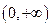 上有唯一的极小值点
上有唯一的极小值点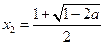 ;
;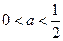 时,
时, 有一个极大值点
有一个极大值点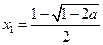 和一个极小值点
和一个极小值点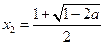 ;
;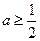 时,函数
时,函数 在
在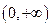 上无极值点。(12分)
上无极值点。(12分)
练习册系列答案
相关题目
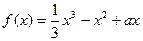 ,
,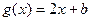 ,当
,当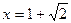 时,
时,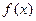 取得极值;
取得极值;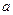 的值,并判断
的值,并判断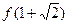 是函数
是函数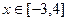 时,函数
时,函数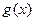 的图象有两个公共点,求
的图象有两个公共点,求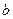 的取值范围;
的取值范围;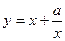 有如下性质:如果常数
有如下性质:如果常数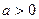 ,那么该函数在
,那么该函数在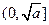 上是减函数,
上是减函数,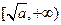 上是增函数,
上是增函数,
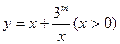 的值域是
的值域是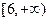 ,求实数
,求实数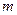 的值;
的值;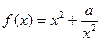 (常数
(常数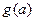 ,
,
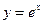 在点
在点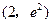 处的切线与坐标轴所围三角形的面积为 ( )
处的切线与坐标轴所围三角形的面积为 ( )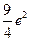
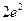
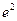
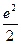
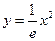 相切于
相切于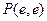 处的切线方程是(其中
处的切线方程是(其中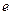 是自然对数的底)( )
是自然对数的底)( )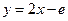



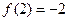 ,
,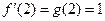 ,
,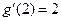 ,则函数
,则函数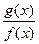 在
在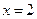 处的导数值为
处的导数值为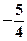
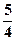
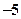
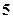
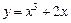 上一点
上一点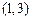 的切线方程是 ▲ .
的切线方程是 ▲ .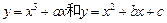 都经过点P(1,2),且在点P处有公切线,则当
都经过点P(1,2),且在点P处有公切线,则当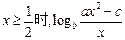 的最小值为( )
的最小值为( )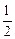
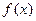 在R上满足
在R上满足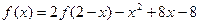 ,则曲线
,则曲线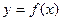 在点
在点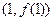 处的切线方程是( )
处的切线方程是( )