题目内容
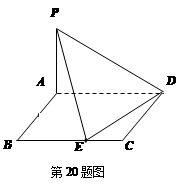
(本题满分12分如图,四边形 为矩形,且
为矩形,且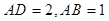 ,
,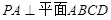 ,
,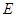 为
为 上的动点。
上的动点。
(1) 当 为
为 的中点时,求证:
的中点时,求证: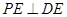 ;
;
(2) 设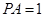 ,在线段
,在线段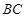 上存在这样的点E,使得二面角
上存在这样的点E,使得二面角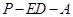 的平面角大小为
的平面角大小为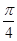 。试确定点E的位置。
。试确定点E的位置。
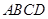 为矩形,且
为矩形,且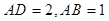 ,
,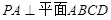 ,
,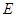 为
为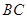 上的动点。
上的动点。
(1) 当
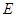 为
为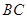 的中点时,求证:
的中点时,求证: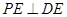 ;
;(2) 设
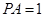 ,在线段
,在线段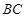 上存在这样的点E,使得二面角
上存在这样的点E,使得二面角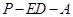 的平面角大小为
的平面角大小为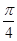 。试确定点E的位置。
。试确定点E的位置。方法一:(1) 证明:当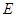 为
为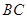 的中点时,
的中点时,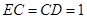 ,
,
从而 为等腰直角三角形,
为等腰直角三角形,
则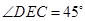 ,同理可得
,同理可得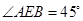 ,∴
,∴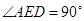 ,于是
,于是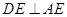 ,………1分
,………1分
又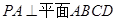 ,且
,且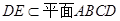 ,∴
,∴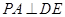 ,
,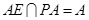 。………2分
。………2分
∴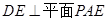 ,又
,又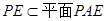 ,∴
,∴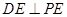 。……………………4分
。……………………4分
(也可以利用三垂线定理证明,但必需指明三垂线定理)
(还可以分别算出PE,PD,DE三条边的长度,再利用勾股定理的逆定理得证,也给满分)(2) 如图过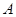 作
作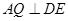 于
于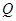 ,连
,连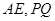 ,则
,则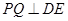 ,………………………6分
,………………………6分
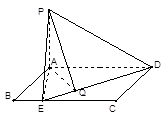
∴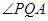 为二面角
为二面角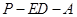 的平面角. ……………8分
的平面角. ……………8分
设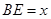 ,则
,则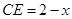 .
.
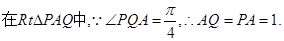 ……………9分
……………9分
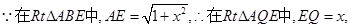
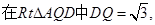 于是
于是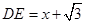 ………………………………10分
………………………………10分
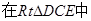 ,有
,有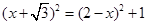 解之得
解之得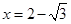 。
。
点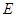 在线段BC上距B点的
在线段BC上距B点的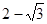 处。………………………12分
处。………………………12分
方法二、向量方法.以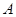 为原点,
为原点,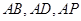 所在直线为
所在直线为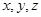 轴,建立空间直角坐标系,如图………………………………1分
轴,建立空间直角坐标系,如图………………………………1分
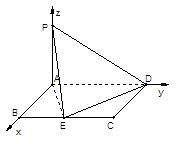
(1)不妨设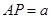 ,则
,则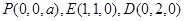 ,
,
从而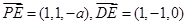 ,………………………2分
,………………………2分
于是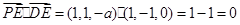 ,
,
所以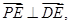 所以
所以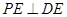 ………………………………4分
………………………………4分
(2)设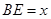 ,则
,则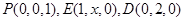 ,
,
则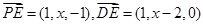 ………………………………………………6分
………………………………………………6分
易知向量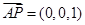 为平面
为平面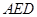 的一个法向量.设平面
的一个法向量.设平面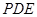 的法向量为
的法向量为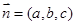 ,
,
则应有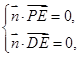 即
即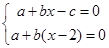 解之得
解之得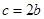 ,令
,令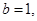 则
则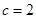 ,
,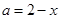 ,
,
从而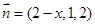 ,………………………………………………………………10分
,………………………………………………………………10分
依题意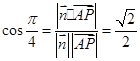 ,即
,即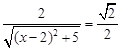 ,
,
解之得 (舍去),
(舍去),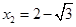 ………………………………………………11分
………………………………………………11分
所以点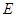 在线段BC上距B点的
在线段BC上距B点的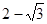 处。………………………………………………12分
处。………………………………………………12分
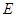 为
为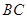 的中点时,
的中点时,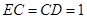 ,
,从而
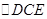 为等腰直角三角形,
为等腰直角三角形,则
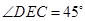 ,同理可得
,同理可得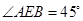 ,∴
,∴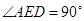 ,于是
,于是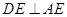 ,………1分
,………1分又
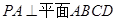 ,且
,且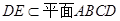 ,∴
,∴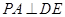 ,
,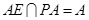 。………2分
。………2分∴
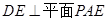 ,又
,又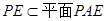 ,∴
,∴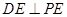 。……………………4分
。……………………4分(也可以利用三垂线定理证明,但必需指明三垂线定理)
(还可以分别算出PE,PD,DE三条边的长度,再利用勾股定理的逆定理得证,也给满分)(2) 如图过
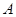 作
作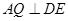 于
于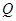 ,连
,连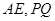 ,则
,则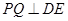 ,………………………6分
,………………………6分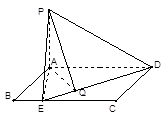
∴
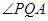 为二面角
为二面角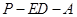 的平面角. ……………8分
的平面角. ……………8分设
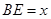 ,则
,则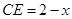 .
.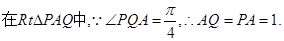 ……………9分
……………9分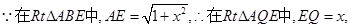
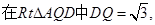 于是
于是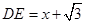 ………………………………10分
………………………………10分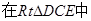 ,有
,有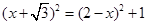 解之得
解之得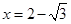 。
。点
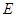 在线段BC上距B点的
在线段BC上距B点的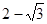 处。………………………12分
处。………………………12分方法二、向量方法.以
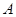 为原点,
为原点,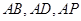 所在直线为
所在直线为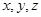 轴,建立空间直角坐标系,如图………………………………1分
轴,建立空间直角坐标系,如图………………………………1分
(1)不妨设
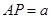 ,则
,则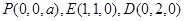 ,
,从而
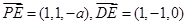 ,………………………2分
,………………………2分于是
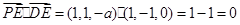 ,
,所以
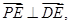 所以
所以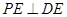 ………………………………4分
………………………………4分(2)设
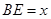 ,则
,则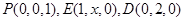 ,
,则
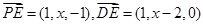 ………………………………………………6分
………………………………………………6分易知向量
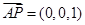 为平面
为平面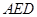 的一个法向量.设平面
的一个法向量.设平面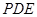 的法向量为
的法向量为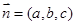 ,
,则应有
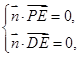 即
即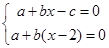 解之得
解之得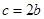 ,令
,令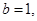 则
则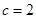 ,
,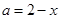 ,
,从而
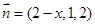 ,………………………………………………………………10分
,………………………………………………………………10分依题意
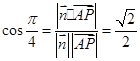 ,即
,即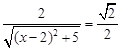 ,
,解之得
 (舍去),
(舍去),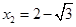 ………………………………………………11分
………………………………………………11分所以点
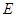 在线段BC上距B点的
在线段BC上距B点的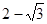 处。………………………………………………12分
处。………………………………………………12分略

练习册系列答案
 波波熊暑假作业江西人民出版社系列答案
波波熊暑假作业江西人民出版社系列答案 学而优暑期衔接南京大学出版社系列答案
学而优暑期衔接南京大学出版社系列答案 Happy holiday欢乐假期暑假作业广东人民出版社系列答案
Happy holiday欢乐假期暑假作业广东人民出版社系列答案
相关题目
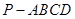 的底面
的底面 是矩形,
是矩形,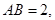
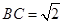 ,且侧面
,且侧面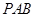 是正三角形,平面
是正三角形,平面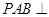 平面
平面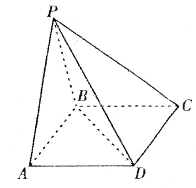
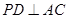 ;
;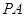 上是否存在一点
上是否存在一点 ,使得二面角
,使得二面角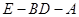 的大小为45°.若存在,试求
的大小为45°.若存在,试求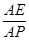 的值,若不存在,请说明理由.
的值,若不存在,请说明理由.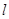 、
、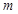 是两条不同的直线,
是两条不同的直线,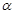 是一个平面,则下列命题正确的是
是一个平面,则下列命题正确的是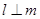 ,
,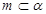 ,则
,则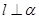
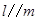 ,则
,则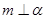
 ,
,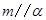 ,则
,则
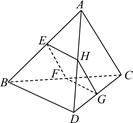
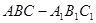 中,
中,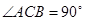 ,
,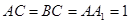 ,
,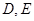 分别为棱
分别为棱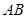 、
、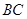 的中点,
的中点,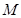 为棱
为棱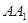 上的点。
上的点。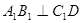 ;
;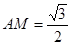 时,求二面角
时,求二面角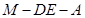 的大小。
的大小。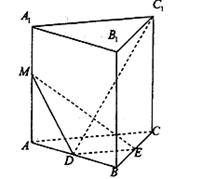
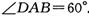 ,菱形ABCD的两条对角线的交点为0,PA=PC,PB=PD,且PO=3.点E是线段PA的中点,连接EO、EB、EC.
,菱形ABCD的两条对角线的交点为0,PA=PC,PB=PD,且PO=3.点E是线段PA的中点,连接EO、EB、EC.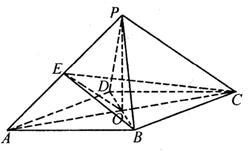
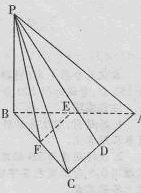
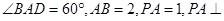 平面ABCD,E是PC的中点,F是AB的中点。
平面ABCD,E是PC的中点,F是AB的中点。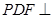 平面PAB;
平面PAB;