题目内容
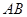 是
是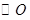 的直径,点
的直径,点 是
是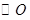 上的动点(点
上的动点(点 不与
不与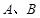 重合),过动点
重合),过动点 的直线
的直线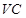 垂直于
垂直于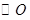 所在的平面,
所在的平面,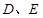 分别是
分别是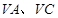 的中点,则下列结论错误的是
的中点,则下列结论错误的是 A.直线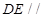 平面 平面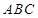 | B.直线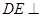 平面 平面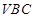 |
C.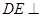 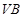 | D.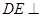 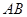 |
D
解:利用直径所对的圆周角为直角,以及线面垂直的性质定理,可以判定,正确的命题为直线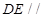 平面
平面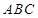 和 直线
和 直线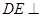 平面
平面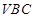
以及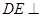
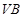 ,而选项D不成立。
,而选项D不成立。
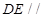 平面
平面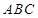 和 直线
和 直线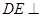 平面
平面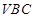
以及
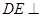
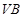 ,而选项D不成立。
,而选项D不成立。
练习册系列答案
 同步练习强化拓展系列答案
同步练习强化拓展系列答案
相关题目
题目内容
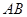 是
是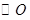 的直径,点
的直径,点 是
是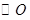 上的动点(点
上的动点(点 不与
不与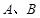 重合),过动点
重合),过动点 的直线
的直线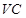 垂直于
垂直于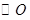 所在的平面,
所在的平面,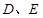 分别是
分别是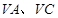 的中点,则下列结论错误的是
的中点,则下列结论错误的是 A.直线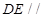 平面 平面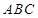 | B.直线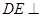 平面 平面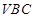 |
C.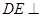 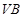 | D.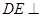 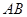 |
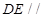 平面
平面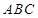 和 直线
和 直线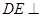 平面
平面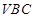
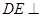
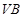 ,而选项D不成立。
,而选项D不成立。
 同步练习强化拓展系列答案
同步练习强化拓展系列答案