题目内容
【题目】已知函数![]() 是定义在区间
是定义在区间![]() 上的奇函数,且
上的奇函数,且![]() ,若对于任意的m,
,若对于任意的m,![]() 有
有![]() .
.
(1)判断函数的单调性(不要求证明);
(2)解不等式![]() ;
;
(3)若![]() 对于任意的
对于任意的![]() ,
,![]() 恒成立,求实数t的取值范围.
恒成立,求实数t的取值范围.
【答案】(1)函数![]() 在区间
在区间![]() 上是减函数;(2)
上是减函数;(2)![]() ;(3)
;(3)![]() .
.
【解析】
(1)设![]() ,化简得到
,化简得到![]() ,结合函数的单调性的定义,即可得到结论;
,结合函数的单调性的定义,即可得到结论;
(2)由(1)知函数![]() 在区间
在区间![]() 上是减函数,根据
上是减函数,根据![]() ,列出不等式组,即可求解不等式的解集;
,列出不等式组,即可求解不等式的解集;
(3)要使得对于任意的![]() ,
,![]() 都有
都有![]() 恒成立,只需对任意的
恒成立,只需对任意的![]() ,
,![]() 恒成立,再结合关于a的一次函数的性质,即可求解.
恒成立,再结合关于a的一次函数的性质,即可求解.
(1)函数![]() 在区间
在区间![]() 上是减函数.
上是减函数.
证明:由题意可知,对于任意的m,![]() 有
有![]() ,
,
设![]() ,则
,则![]() ,即
,即![]() ,
,
当![]() 时,
时,![]() ,所以函数在
,所以函数在![]() 上为单调递减函数;
上为单调递减函数;
当![]() 时,
时,![]() ,所以函数在
,所以函数在![]() 上为单调递减函数,
上为单调递减函数,
综上,函数![]() 在
在![]() 上为单调递减函数.
上为单调递减函数.
(2)由(1)知函数![]() 在区间
在区间![]() 上是减函数,
上是减函数,
因为![]() ,可得
,可得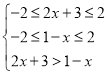 ,解得解得
,解得解得![]() ,
,
所以不等式![]() 的解集为
的解集为![]() .
.
(3)因为函数![]() 在区间
在区间![]() 上是减函数,且
上是减函数,且![]() ,
,
要使得对于任意的![]() ,
,![]() 都有
都有![]() 恒成立,
恒成立,
只需对任意的![]() ,
,![]() 恒成立.
恒成立.
令![]() ,此时y可以看作a的一次函数,且在
,此时y可以看作a的一次函数,且在![]() 时,
时,![]() 恒成立.
恒成立.
因此只需![]() ,解得解得
,解得解得![]() ,
,
所以实数t的取值范围为![]() .
.

练习册系列答案
 轻松夺冠全能掌控卷系列答案
轻松夺冠全能掌控卷系列答案
相关题目