题目内容
10.用弧度表示终边落在如图所示的阴影部分内(不包括边界)的角的集合.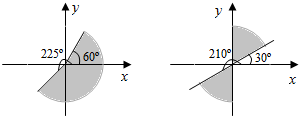
分析 图一中,利用终边相同的角的集合定理可得出分别与角$\frac{π}{3}$,$\frac{5π}{4}$终边相同的角,即可终边落在阴影区域(不包括边界)的角的集合;图二中,终边落在如图所示的阴影部分内(不包括边界)的角分别位于一、三象限,在第一象限内,$\frac{π}{6}$<α<$\frac{π}{2}$,在第二象限,$\frac{7π}{6}$<α<$\frac{3π}{2}$,由此能求出终边落在如图所示的阴影部分内(不包括边界)的角的集合.
解答 解:在第一个图形中,
分别与角$\frac{π}{3}$,$\frac{5π}{4}$终边相同的角为$\frac{π}{3}$+2kπ,-$\frac{3π}{4}$+2kπ(k∈Z).
因此终边落在阴影区域(不包括边界)的角的集合是:
{α|-$\frac{3π}{4}$+2kπ<α<$\frac{π}{3}$+2kπ,k∈Z}.
在第二个图形中,终边落在如图所示的阴影部分内(不包括边界)的角分别位于一、三象限,
在第一象限内,$\frac{π}{6}$<α<$\frac{π}{2}$,在第二象限,$\frac{7π}{6}$<α<$\frac{3π}{2}$,
∴终边落在如图所示的阴影部分内(不包括边界)的角的集合为:
{α|$\frac{π}{6}$+2kπ<α<$\frac{π}{2}$+2kπ,或$\frac{7π}{6}$+2kπ<α<$\frac{3π}{2}$+2kπ,k∈Z}={α|$\frac{π}{6}$+kπ<α<$\frac{π}{2}$+kπ,k∈Z}.
点评 本题考查终边相同的角的集合的求法,是基础题,解题时要认真审题,注意终边相同的角的集合的合理运用.

练习册系列答案
 口算题天天练系列答案
口算题天天练系列答案
相关题目
2.设向量$\overrightarrow{a}$与$\overrightarrow{b}$不共线.已知命题p:向量$\overrightarrow{a}$,$\overrightarrow{b}$,$\overrightarrow{c}$共面;命题q:存在两个非零常数λ,μ,使c=λ$\overrightarrow{a}$+μ$\overrightarrow{b}$.则p是q的( )
| A. | 充分而不必要条件 | B. | 必要而不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
19.定义在R上的偶函数f(x)满足f(4)=f(-2)=0,在区间(-∞,-3)与[-3,0]上分别递增和递减,则不等式xf(x)>0的解集为( )
| A. | (-∞,-4)∪(4,+∞) | B. | (-4,-2)∪(2,4) | C. | (-∞,-4)∪(-2,0) | D. | (-∞,-4)∪(-2,0)∪(2,4) |