题目内容
【题目】下列五个命题:
①“![]() ”是“
”是“![]() 为R上的增函数”的充分不必要条件;
为R上的增函数”的充分不必要条件;
②函数![]() 有两个零点;
有两个零点;
③集合![]() ,
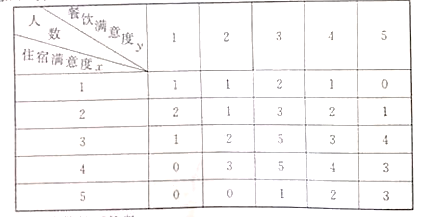
,![]() ,从A,B中各任意取一个数,则这两数之和等于4的概率是
,从A,B中各任意取一个数,则这两数之和等于4的概率是![]() ;
;
④动圆C既与定圆![]() 相外切,又与y轴相切,则圆心C的轨迹方程是
相外切,又与y轴相切,则圆心C的轨迹方程是![]() ;
;
⑤若对任意的正数x,不等式![]() 恒成立,则实数a的取值范围是
恒成立,则实数a的取值范围是![]() .
.
其中正确的命题序号是________.
【答案】①③⑤
【解析】
①用导数法求出![]() 在R上的增函数的充要条件,与
在R上的增函数的充要条件,与![]() 对比即可判断结果;②求出函数
对比即可判断结果;②求出函数![]() 的极值,并判断正负,即可判断结论;
的极值,并判断正负,即可判断结论;
③列出从A,B中各任意取一个数所有情况,算出两数之和等于4的基本事件,即可求出概率,判断结论真假;
④按求轨迹的方法求出动点轨迹方程,即可判断结论,或举出反例;
⑤构造函数![]() ,求出最小值或取值范围,进而得出
,求出最小值或取值范围,进而得出![]() 的范围,即可判断命题真假.
的范围,即可判断命题真假.
①![]() 在R上的增函数,
在R上的增函数,
![]() 恒成立,
恒成立,![]() .
.
“![]() ”是“
”是“![]() ”的充分不必要条件,所以①正确;
”的充分不必要条件,所以①正确;
②![]() ,
,
![]() 或
或![]() ,
,
![]() 递增区间是
递增区间是![]() ,递减区间是
,递减区间是![]() ,
,
![]() 极大值为
极大值为![]() 的极小值为
的极小值为![]() ,
,
![]() 只有一个零点,②不正确;
只有一个零点,②不正确;
③集合![]() ,
,![]() ,从A,B中各任意取一个数,
,从A,B中各任意取一个数,
所以情况有![]() 共6种取法,
共6种取法,
两数之和等于4有2种取法,所以概率为![]() ,③正确;
,③正确;
④设圆心![]() ,定圆
,定圆![]() 圆心为
圆心为![]() ,
,
半径为2,依题意![]() ,平方化简得
,平方化简得
![]() ,当
,当![]() 时,
时,![]() ,当
,当![]() ,
,
![]() 在定圆上不合题意,当
在定圆上不合题意,当![]() 时,
时,![]() ,④不正确;
,④不正确;
⑤设![]()
在![]() 上恒成立,
上恒成立,![]() 单调递增,
单调递增,
![]() ,不等式
,不等式![]() 在
在![]() 上恒成立,
上恒成立,
![]() ,⑤正确.
,⑤正确.
故答案为:①③⑤.

 精英口算卡系列答案
精英口算卡系列答案 应用题点拨系列答案
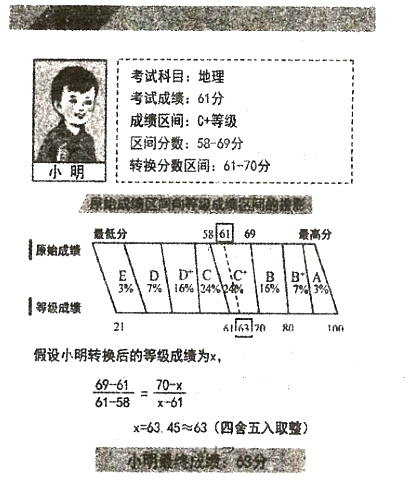
应用题点拨系列答案【题目】《山东省高考改革试点方案》规定:从![]() 年高考开始,高考物理、化学等六门选考科目的考生原始成绩从高到低划分为
年高考开始,高考物理、化学等六门选考科目的考生原始成绩从高到低划分为![]() 八个等级.参照正态分布原则,确定各等级人数所占比例分别为
八个等级.参照正态分布原则,确定各等级人数所占比例分别为![]() .选考科目成绩计入考生总成绩时,将
.选考科目成绩计入考生总成绩时,将![]() 至
至![]() 等级内的考生原始成绩,依照等比例转换法则分别转换到
等级内的考生原始成绩,依照等比例转换法则分别转换到![]()
![]() 八个分数区间,得到考生的等级成绩.
八个分数区间,得到考生的等级成绩.
某校![]() 级学生共
级学生共![]() 人,以期末考试成绩为原始成绩转换了本校的等级成绩,为学生合理选科提供依据,其中物理成绩获得等级
人,以期末考试成绩为原始成绩转换了本校的等级成绩,为学生合理选科提供依据,其中物理成绩获得等级![]() 的学生原始成绩统计如下
的学生原始成绩统计如下
成绩 | 93 | 91 | 90 | 88 | 87 | 86 | 85 | 84 | 83 | 82 |
人数 | 1 | 1 | 4 | 2 | 4 | 3 | 3 | 3 | 2 | 7 |
(1)从物理成绩获得等级![]() 的学生中任取
的学生中任取![]() 名,求恰好有
名,求恰好有![]() 名同学的等级分数不小于
名同学的等级分数不小于![]() 的概率;
的概率;
(2)待到本级学生高考结束后,从全省考生中不放回的随机抽取学生,直到抽到![]() 名同学的物理高考成绩等级为
名同学的物理高考成绩等级为![]() 或
或![]() 结束(最多抽取
结束(最多抽取![]() 人),设抽取的学生个数为
人),设抽取的学生个数为![]() ,求随机变量
,求随机变量![]() 的数学期望(注:
的数学期望(注: ![]() ).
).