题目内容
【题目】已知{an}是由非负整数组成的无穷数列,该数列前n项的最大值记为An , 第n项之后各项an+1 , an+2…的最小值记为Bn , dn=An﹣Bn .
(1)若{an}为2,1,4,3,2,1,4,3…,是一个周期为4的数列(即对任意n∈N* , an+4=an),写出d1 , d2 , d3 , d4的值;
(2)设d是非负整数,证明:dn=﹣d(n=1,2,3…)的充分必要条件为{an}是公差为d的等差数列;
(3)证明:若a1=2,dn=1(n=1,2,3,…),则{an}的项只能是1或者2,且有无穷多项为1.
【答案】
(1)解:若{an}为2,1,4,3,2,1,4,3…,是一个周期为4的数列,∴d1=A1﹣B1=2﹣1=1,
d2=A2﹣B2=2﹣1=1,d3=A3﹣B3=4﹣1=3,d4=A4﹣B4=4﹣1=3.
(2)证明:
充分性:设d是非负整数,若{an}是公差为d的等差数列,则an=a1+(n﹣1)d,
∴An=an=a1+(n﹣1)d,Bn=an+1=a1+nd,∴dn=An﹣Bn=﹣d,(n=1,2,3,4…).
必要性:若 dn=An﹣Bn=﹣d,(n=1,2,3,4…).假设ak是第一个使ak﹣ak﹣1<0的项,
则dk=Ak﹣Bk=ak﹣1﹣Bk≥ak﹣1﹣ak>0,这与dn=﹣d≤0相矛盾,故{an}是一个不减的数列.
∴dn=An﹣Bn=an﹣an+1=﹣d,即 an+1﹣an=d,故{an}是公差为d的等差数列.
(3)证明:若a1=2,dn=1(n=1,2,3,…),首先,{an}的项不能等于零,否则d1=2﹣0=2,矛盾.
而且还能得到{an}的项不能超过2,用反证法证明如下:
假设{an}的项中,有超过2的,设am是第一个大于2的项,由于{an}的项中一定有1,否则与d1=1矛盾.
当n≥m时,an≥2,否则与dm=1矛盾.
因此,存在最大的i在2到m﹣1之间,使ai=1,此时,di=Ai﹣Bi=2﹣Bi≤2﹣2=0,矛盾.
综上,{an}的项不能超过2,故{an}的项只能是1或者2.
下面用反证法证明{an}的项中,有无穷多项为1.
若ak是最后一个1,则ak是后边的各项的最小值都等于2,故dk=Ak﹣Bk=2﹣2=0,矛盾,
故{an}的项中,有无穷多项为1.
综上可得,{an}的项只能是1或者2,且有无穷多项为1.
【解析】(1)根据条件以及dn=An﹣Bn的定义,直接求得d1 , d2 , d3 , d4的值.(2)设d是非负整数,若{an}是公差为d的等差数列,则an=a1+(n﹣1)d,从而证得dn=An﹣Bn=﹣d,(n=1,2,3,4…).若dn=An﹣Bn=﹣d,(n=1,2,3,4…).可得{an}是一个不减的数列,求得dn=An﹣Bn=﹣d,即 an+1﹣an=d,即{an}是公差为d的等差数列,命题得证.(3)若a1=2,dn=1(n=1,2,3,…),则{an}的项不能等于零,再用反证法得到{an}的项不能超过2,
从而证得命题.
【考点精析】关于本题考查的等差关系的确定和等比关系的确定,需要了解如果一个数列从第2项起,每一项与它的前一项的差等于同一个常数,即![]() -
-![]() =d ,(n≥2,n∈N
=d ,(n≥2,n∈N![]() )那么这个数列就叫做等差数列;等比数列可以通过定义法、中项法、通项公式法、前n项和法进行判断才能得出正确答案.
)那么这个数列就叫做等差数列;等比数列可以通过定义法、中项法、通项公式法、前n项和法进行判断才能得出正确答案.

【题目】为了了解我市特色学校的发展状况,某调查机构得到如下统计数据:
年份 | 2014 | 2015 | 2016 | 2017 | 2018 |
特色学校 | 0.30 | 0.60 | 1.00 | 1.40 | 1.70 |
(Ⅰ)根据上表数据,计算![]() 与
与![]() 的相关系数
的相关系数![]() ,并说明
,并说明![]() 与
与![]() 的线性相关性强弱(已知:
的线性相关性强弱(已知:![]() ,则认为
,则认为![]() 与
与![]() 线性相关性很强;
线性相关性很强;![]() ,则认为
,则认为![]() 与
与![]() 线性相关性一般;
线性相关性一般;![]() ,则认为
,则认为![]() 与
与![]() 线性相关性较弱);
线性相关性较弱);
(Ⅱ)求![]() 关于
关于![]() 的线性回归方程,并预测我市2019年特色学校的个数(精确到个).
的线性回归方程,并预测我市2019年特色学校的个数(精确到个).
参考公式: 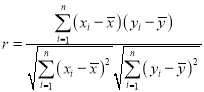 ,
,![]() ,
,![]() ,
,![]() ,
,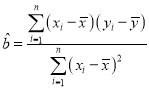 ,
,![]() .
.
【题目】为了评估A,B两家快递公司的服务质量,从两家公司的客户中各随机抽取100名客户作为样本,进行服务质量满意度调查,将A,B两公司的调查得分分别绘制成频率分布表和频率分布直方图.规定![]() 分以下为对该公司服务质量不满意.
分以下为对该公司服务质量不满意.
分组 | 频数 | 频率 |
|
|
|
|
|
|
|
| 0.4 |
|
|
|
|
|
|
合计 |
|
|

(Ⅰ)求样本中对B公司的服务质量不满意的客户人数;
(Ⅱ)现从样本对A,B两个公司服务质量不满意的客户中,随机抽取2名进行走访,求这两名客户都来自于B公司的概率;
(Ⅲ)根据样本数据,试对两个公司的服务质量进行评价,并阐述理由.

