题目内容
11.画出不等式组$\left\{\begin{array}{l}-x+y-2≤0\\ x+y-4≤0\\ x-3y+3≤0\end{array}\right.$表示的平面区域,若z=x+y,求出z的最大值和最小值.分析 作出原不等式所对应的平面区域,变形目标函数可得y=-x+z,平移直线y=-x代点的坐标计算可得最值.
解答 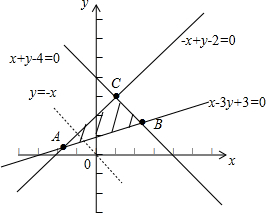 解:作出原不等式所对应的平面区域,(如图阴影),
解:作出原不等式所对应的平面区域,(如图阴影),
变形目标函数可得y=-x+z,平移直线y=-x可知:
当直线经过点A(-$\frac{3}{2}$,$\frac{1}{2}$)时,直线的截距最小即z最小,
代值计算可得zmin=-$\frac{3}{2}$+$\frac{1}{2}$=-1;
当直线经过线段BC,不妨取B($\frac{9}{4}$,$\frac{7}{4}$)时,直线的截距最大即z最大,
代值计算可得zmax=$\frac{9}{4}$+$\frac{7}{4}$=4
∴z的最大值和最小值分别为4,-1
点评 本题考查简单线性规划,准确作图是解决问题的关键,属中档题.

练习册系列答案
相关题目
3.在△ABC中,A、B、C的对边分别为a、b、c,且bcosC=3acosB-ccosB,$\overrightarrow{BA}$•$\overrightarrow{BC}$=2,则△ABC的面积为( )
| A. | $\sqrt{2}$ | B. | $\frac{3}{2}$ | C. | 2$\sqrt{2}$ | D. | 4$\sqrt{2}$ |
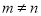 ,两个等差数列
,两个等差数列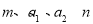 与
与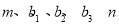 的公差为
的公差为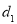 和
和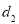 ,则
,则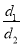 的值为________.
的值为________.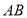 是
是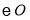 的直径,
的直径,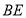 为
为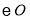 的切线,点
的切线,点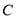 为
为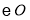 上不同于
上不同于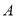 、
、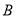 的一点,
的一点,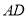 为
为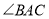 的平分线,且分别与
的平分线,且分别与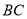 交于
交于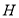 ,与
,与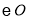 交于
交于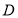 ,与
,与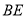 交于
交于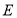 ,连接
,连接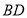 、
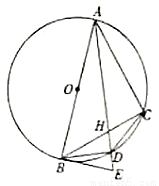
、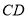 .
.
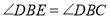 ;
;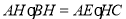 .
.