题目内容
16.一束光线沿着直线y=-3x+b射到直线x+y=0上,经反射后沿着直线y=ax+2射出,求a,b的值.分析 由直线的对称性可得三线共点,可得到角相等,进而可得ab的方程组,解方程组可得ab的值.
解答 解:联立$\left\{\begin{array}{l}{y=-3x+b}\\{x+y=0}\end{array}\right.$可解得$\left\{\begin{array}{l}{x=\frac{b}{2}}\\{y=-\frac{b}{2}}\end{array}\right.$,即直线交点为($\frac{b}{2}$,-$\frac{b}{2}$),
代入y=ax+2可得-$\frac{b}{2}$=$\frac{ab}{2}$+2,即ab+b+4=0 (1),
由对称性可得到角相等,可得$\frac{-1-(-3)}{1+(-1)(-3)}$=$\frac{a-(-1)}{1+a(-1)}$,解得a=$-\frac{1}{3}$
代入(1)可解得b=-6
∴ab的值分别为$-\frac{1}{3}$,-6
点评 本题考查直线的对称性,涉及到角公式,属基础题.

练习册系列答案
相关题目
 (
( ,
, 为常数,
为常数, )满足
)满足 ,且
,且 有唯一解.
有唯一解. 的解析式;
的解析式; ,且
,且 (
( ,
, ),求证:数列
),求证:数列 为等差数列.
为等差数列. 如图,在平面直角坐标系xOy中,已知椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率为$\frac{\sqrt{2}}{2}$,且右焦点F到左准线l的距离为3.
如图,在平面直角坐标系xOy中,已知椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率为$\frac{\sqrt{2}}{2}$,且右焦点F到左准线l的距离为3. 满足:
满足: ,
, ,而数列
,而数列 项和数值最大时,
项和数值最大时, 的值为( )
的值为( )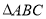 中,内角
中,内角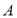 ,
,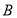 ,
,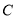 的对边分别为
的对边分别为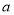 ,
,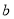 ,
,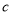 ,且
,且 ,已知
,已知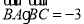 ,
,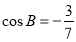 ,
, .求:
.求: 和
和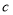 的值;
的值;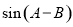 的值.
的值.