题目内容
4．若2b2-a2=4，求|a-2b|的最小值．分析 由于（a-2b）2=a2+4b2-4ab，利用基本不等式即可得答案．
解答 解：（a-2b）2=a2+4b2-4ab≥a2+4b2-2（a2+b2）=2b2-a2=4，当且仅当a=b=2时取等号，
故|a-2b|的最小值为2．
点评 本题考查了基本不等式的应用，注意等号成立的条件，属于基础题．
练习册系列答案
备战中考寒假系列答案
相关题目
14．
一个三棱锥的三视图如图所示，其中俯视图为等腰直角三角形，正视图和侧视图是全等的等腰三角形，则此三棱外接球的表面积为（ ）
一个三棱锥的三视图如图所示，其中俯视图为等腰直角三角形，正视图和侧视图是全等的等腰三角形，则此三棱外接球的表面积为（ ）| A． | 16π | B． | 9π | C． | 4π | D． | π |
12．已知双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1（a＞0，b＞0）的左焦点与抛物线y2=-8x的焦点重合，斜率为1的直线l与双曲线交于A、B两点，若A，B中点坐标为（-3，-1），则该双曲线的离心率为（ ）
| A． | $\sqrt{2}$ | B． | $\frac{3\sqrt{2}}{2}$ | C． | $\sqrt{3}$ | D． | $\frac{2}{3}$$\sqrt{3}$ |
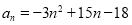，则数列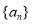
中的最大项的值是（ ）
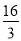B．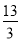
C．4 D．0