题目内容
2.已知矩阵A=$[\begin{array}{l}{-1}&{0}\\{0}&{2}\end{array}]$,B=$[\begin{array}{l}{1}&{2}\\{0}&{6}\end{array}]$,求矩阵A-1B.分析 设矩阵A-1=$[\begin{array}{l}{a}&{b}\\{c}&{d}\end{array}]$,通过AA-1为单位矩阵可得A-1,进而可得结论.
解答 解:设矩阵A的逆矩阵为$[\begin{array}{l}{a}&{b}\\{c}&{d}\end{array}]$,
则$[\begin{array}{l}{-1}&{0}\\{0}&{2}\end{array}]$$[\begin{array}{l}{a}&{b}\\{c}&{d}\end{array}]$=$[\begin{array}{l}{1}&{0}\\{0}&{1}\end{array}]$,即$[\begin{array}{l}{-a}&{-b}\\{2c}&{2d}\end{array}]$=$[\begin{array}{l}{1}&{0}\\{0}&{1}\end{array}]$,
故a=-1,b=0,c=0,d=$\frac{1}{2}$,
从而A-1=$[\begin{array}{l}{-1}&{0}\\{0}&{\frac{1}{2}}\end{array}]$,
∴A-1B=$[\begin{array}{l}{-1}&{0}\\{0}&{\frac{1}{2}}\end{array}]$$[\begin{array}{l}{1}&{2}\\{0}&{6}\end{array}]$=$[\begin{array}{l}{-1}&{-2}\\{0}&{3}\end{array}]$.
点评 本题考查逆矩阵、矩阵的乘法,考查运算求解能力,属于基础题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
18.设f(x)是定义在R上的偶函数,且当x≥0时,f(x)=$\left\{\begin{array}{l}{{x}^{2}-1,0≤x<1}\\{lnx,x≥1}\end{array}\right.$,若对任意的x∈[a,a+1],不等式f(2x)≤f(x+a)恒成立,则实数a的最大值为( )
| A. | -1 | B. | -$\frac{2}{3}$ | C. | -$\frac{1}{2}$ | D. | -$\frac{3}{4}$ |
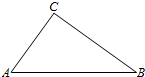 如图,A,B,C三地有直道相通,AB=5千米,AC=3千米,BC=4千米.现甲、乙两警员同时从A地出发匀速前往B地,经过t小时,他们之间的距离为f(t)(单位:千米).甲的路线是AB,速度为5千米/小时,乙的路线是ACB,速度为8千米/小时.乙到达B地后原地等待.设t=t1时乙到达C地.
如图,A,B,C三地有直道相通,AB=5千米,AC=3千米,BC=4千米.现甲、乙两警员同时从A地出发匀速前往B地,经过t小时,他们之间的距离为f(t)(单位:千米).甲的路线是AB,速度为5千米/小时,乙的路线是ACB,速度为8千米/小时.乙到达B地后原地等待.设t=t1时乙到达C地. ,则数列
,则数列 中的最大项的值是( )
中的最大项的值是( ) B.
B. C.4 D.0
C.4 D.0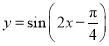 的图象向左平移
的图象向左平移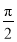 个单位长度,所得图象对应的函数( )
个单位长度,所得图象对应的函数( )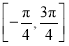 上单调递减 B.在区间
上单调递减 B.在区间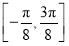 上单调递减 D.在区间
上单调递减 D.在区间