题目内容
【题目】如图,已知四棱锥P﹣ABCD,底面ABCD为边长为2对的菱形,PA⊥平面ABCD,∠ABC=60°,E,F分别是BC,PC的中点. 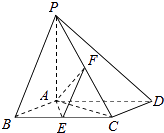
(1)判定AE与PD是否垂直,并说明理由;
(2)若PA=2,求二面角E﹣AF﹣C的余弦值.
【答案】
(1)解:垂直.
证明:由四边形ABCD为菱形,∠ABC=60°,
可得△ABC为正三角形.
因为E为BC的中点,所以AE⊥BC.
又BC∥AD,因此AE⊥AD.
因为PA⊥平面ABCD,AE平面ABCD,
所以PA⊥AE.
而PA平面PAD,AD平面PAD且PA∩AD=A,
所以AE⊥平面PAD,又PD平面PAD,
所以AE⊥PD.
(2)解:由(1)知AE,AD,AP两两垂直,以A为坐标原点,
建立如图所示的空间直角坐标系,又E,F分别为BC,PC的中点,∴A(0,0,0), ![]() ,
, ![]() ,D(0,2,0),P(0,0,2),
,D(0,2,0),P(0,0,2), ![]() ,
,  ,
,
所以 ![]() ,
,  .
.
设平面AEF的一个法向量为 ![]() ,则
,则  ,
,
因此  ,取z1=﹣1,则
,取z1=﹣1,则 ![]() .
.
因为BD⊥AC,BD⊥PA,PA∩AC=A,
所以BD⊥平面AFC,故 ![]() 为平面AFC的一个法向量.
为平面AFC的一个法向量.
又 ![]() ,所以
,所以  .
.
因为二面角E﹣AF﹣C为锐角,所以所求二面角的余弦值为 ![]() .
.

【解析】(1)判断垂直.证明AE⊥BC.PA⊥AE.推出AE⊥平面PAD,然后证明AE⊥PD.(2)由(1)知AE,AD,AP两两垂直,以A为坐标原点,建立如图所示的空间直角坐标系,求出相关点的坐标,求出平面AEF的一个法向量,平面AFC的一个法向量.通过向量的数量积求解二面角的余弦值.
【考点精析】关于本题考查的直线与平面垂直的性质,需要了解垂直于同一个平面的两条直线平行才能得出正确答案.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目