题目内容
11.已知数列满足:a1=1,an+1=$\frac{{a}_{n}}{{a}_{n}+2}$(n∈N*),若bn+1=(n-λ)($\frac{1}{{a}_{n}}$+1),b1=-6,且递增数列,则实数λ的取值范围为λ<3.分析 a1=1,an+1=$\frac{{a}_{n}}{{a}_{n}+2}$(n∈N*),两边取倒数可得:$\frac{1}{{a}_{n+1}}$+1=$2(\frac{1}{{a}_{n}}+1)$,利用等比数列的通项公式可得$\frac{1}{{a}_{n}}$.又bn+1=(n-λ)($\frac{1}{{a}_{n}}$+1)=(n-λ)•2n,又b1=-6,且递增数列,可得b2=(2-λ)•2>b1=-6,n≥2时,bn+1>bn.解出即可得出.
解答 解:∵a1=1,an+1=$\frac{{a}_{n}}{{a}_{n}+2}$(n∈N*),
两边取倒数可得:$\frac{1}{{a}_{n+1}}$=$\frac{2}{{a}_{n}}$+1,变形为$\frac{1}{{a}_{n+1}}$+1=$2(\frac{1}{{a}_{n}}+1)$,
∴数列$\{\frac{1}{{a}_{n}}+1\}$是等比数列,首项为2,公比为2,
∴$\frac{1}{{a}_{n}}$+1=2n,
∴bn+1=(n-λ)($\frac{1}{{a}_{n}}$+1)=(n-λ)•2n,
又b1=-6,且递增数列,
∴b2=(2-λ)•2>b1=-6,n≥2时,bn+1>bn.
化为$\left\{\begin{array}{l}{λ<5}\\{λ<3}\end{array}\right.$,解得λ<3.
∴实数λ的取值范围为λ<3.
故答案为:λ<3.
点评 本题考查了递推关系的应用、等比数列的通项公式、数列的单调性,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
16.已知数列{an}的首项a1=1,且an+1=2an+1,则这个数列的第五项为( )
| A. | 31 | B. | 15 | C. | 11 | D. | 9 |

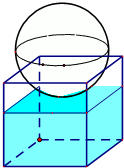 如图,有一个水平放置的透明无盖的正方体容器,容器高8cm,将一个球放在容器口,再向容器内注水,当球面恰好接触水面时测得水深为6cm,如果不计容器的厚度,求球的体积.
如图,有一个水平放置的透明无盖的正方体容器,容器高8cm,将一个球放在容器口,再向容器内注水,当球面恰好接触水面时测得水深为6cm,如果不计容器的厚度,求球的体积.