题目内容
1.已知函数g(x)=x+1,x∈[0,2],f(x)=x2+mx+2.(1)若方程f(x)=-$\frac{1}{2}$m有两个实根x1,x2,求x12+x22的取值范围;
(2)若函数F(x)=f(x)-g(x)有两个零点,求m的取值范围.
分析 (1)方程f(x)=-$\frac{1}{2}$m有两个实根x1,x2,即方程x2+$\frac{3}{2}$mx+2=0有两个实根x1,x2,故△=$\frac{9}{4}{m}^{2}-8≥0$,x1+x2=$-\frac{3}{2}$m,x1•x2=2,进而可得x12+x22的取值范围;
(2)若函数F(x)=f(x)-g(x)有两个零点,即方程x2+mx+2-(x+1)=x2+(m-1)x+1=0有两个不等的实根,故△=(m-1)2-4>0,解得答案.
解答 解:(1)∵方程f(x)=-$\frac{1}{2}$m有两个实根x1,x2,
即方程x2+$\frac{3}{2}$mx+2=0有两个实根x1,x2,
故△=$\frac{9}{4}{m}^{2}-8≥0$,
x1+x2=$-\frac{3}{2}$m,x1•x2=2,
故x12+x22=(x1+x2)2-2x1•x2=$\frac{9}{4}{m}^{2}-4$=$\frac{9}{4}{m}^{2}-8+4$≥0;
(2)若函数F(x)=f(x)-g(x)有两个零点,
即方程x2+mx+2-(x+1)=x2+(m-1)x+1=0有两个不等的实根,
故△=(m-1)2-4>0,解得:m<-1,或m>3.
点评 本题考查的知识点是函数零点与方程的根,转化思想,难度中档.

练习册系列答案
相关题目
6.已知集合A={x|2x2-x-1≤0},集合B={x|y=$\frac{2ln({3}^{x}-1)}{(x-1)^{2}}$},则A∩B=( )
| A. | (0,1) | B. | (0,1] | C. | (1,+∞) | D. | [1,+∞) |
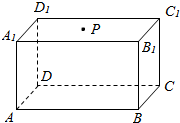 如图,P为长方体ABCD-A1B1C1D1的上底面A1B1C1D1内的一点,过直线BC与点P的平面记为α,若α∩平面A1B1C1D1=l
如图,P为长方体ABCD-A1B1C1D1的上底面A1B1C1D1内的一点,过直线BC与点P的平面记为α,若α∩平面A1B1C1D1=l