题目内容
已知函数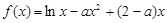 .
.
(I)讨论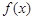 的单调性;
的单调性;
(II)设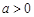 ,证明:当
,证明:当 时,
时,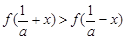 ;
;
(III)若函数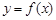 的图像与x轴交于A,B两点,线段AB中点的横坐标为x0,
的图像与x轴交于A,B两点,线段AB中点的横坐标为x0,
证明: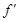 (x0)<0.
(x0)<0.
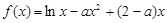 .
.(I)讨论
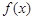 的单调性;
的单调性;(II)设
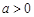 ,证明:当
,证明:当 时,
时,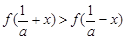 ;
;(III)若函数
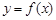 的图像与x轴交于A,B两点,线段AB中点的横坐标为x0,
的图像与x轴交于A,B两点,线段AB中点的横坐标为x0,证明:
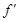 (x0)<0.
(x0)<0.(1)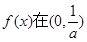 单调增加,在
单调增加,在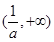 单调减少;
单调减少;
(2)当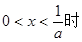 ,
,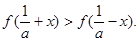
(3)见解析.
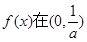 单调增加,在
单调增加,在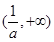 单调减少;
单调减少;(2)当
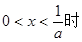 ,
,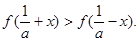
(3)见解析.
第一问利用导数求解得到。
(I)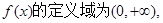
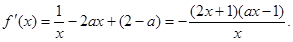
(i)若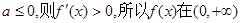 单调增加.
单调增加.
(ii)若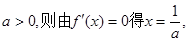 且当
且当
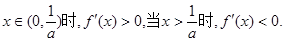
所以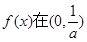 单调增加,在
单调增加,在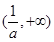 单调减少.
单调减少.
第二问中,构造函数设函数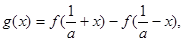 则
则
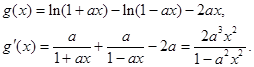
结合导数得到单调性判定进而求解。
第三问中,由(I)可得,当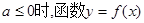 的图像与x轴至多有一个交点,
的图像与x轴至多有一个交点,
故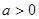 ,从而
,从而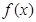 的最大值为
的最大值为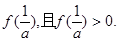
解:(I)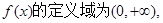
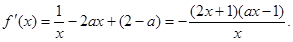
(i)若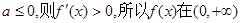 单调增加.
单调增加.
(ii)若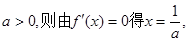 且当
且当
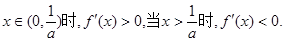
所以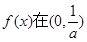 单调增加,在
单调增加,在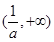 单调减少. 3分
单调减少. 3分
(II)设函数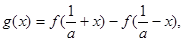 则
则
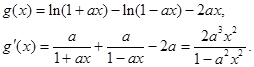
当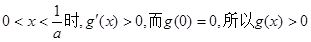 .
.
故当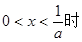 ,
,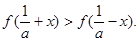 6分
6分
(III)由(I)可得,当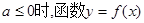 的图像与x轴至多有一个交点,
的图像与x轴至多有一个交点,
故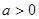 ,从而
,从而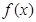 的最大值为
的最大值为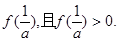
不妨设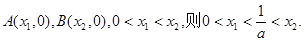
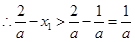
由(II)得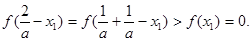 从而
从而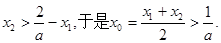
由(I)知,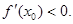 10分
10分
(I)
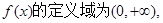
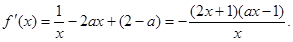
(i)若
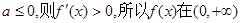 单调增加.
单调增加.(ii)若
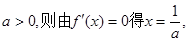 且当
且当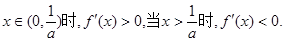
所以
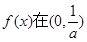 单调增加,在
单调增加,在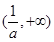 单调减少.
单调减少.第二问中,构造函数设函数
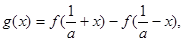 则
则 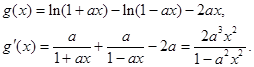
结合导数得到单调性判定进而求解。
第三问中,由(I)可得,当
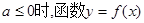 的图像与x轴至多有一个交点,
的图像与x轴至多有一个交点,故
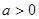 ,从而
,从而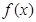 的最大值为
的最大值为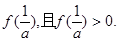
解:(I)
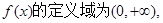
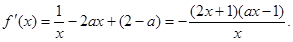
(i)若
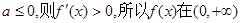 单调增加.
单调增加.(ii)若
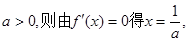 且当
且当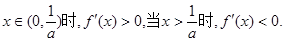
所以
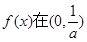 单调增加,在
单调增加,在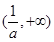 单调减少. 3分
单调减少. 3分(II)设函数
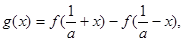 则
则 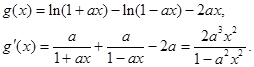
当
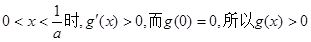 .
.故当
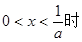 ,
,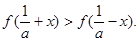 6分
6分(III)由(I)可得,当
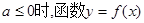 的图像与x轴至多有一个交点,
的图像与x轴至多有一个交点,故
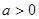 ,从而
,从而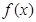 的最大值为
的最大值为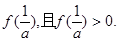
不妨设
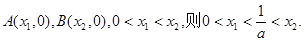
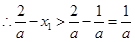
由(II)得
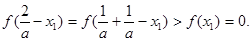 从而
从而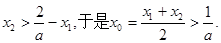
由(I)知,
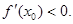 10分
10分
练习册系列答案
 学而优衔接教材南京大学出版社系列答案
学而优衔接教材南京大学出版社系列答案
相关题目
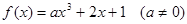 在
在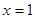 处的切线与直线
处的切线与直线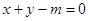 垂直,则
垂直,则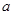 等于
等于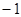
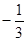
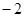
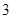
 企
企 业拟建造如图所示的容器(不计厚度,长度单位:米),其中容器的中间为圆柱形,左右两端均为半球形,按照设计要求容器的体积为
业拟建造如图所示的容器(不计厚度,长度单位:米),其中容器的中间为圆柱形,左右两端均为半球形,按照设计要求容器的体积为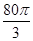 立方米,且
立方米,且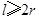 .假设该容器的建造费用仅与其表面积有关.已知圆柱形部分每平方米建造费用为3千元,半球形部分每平方米建造费用为
.假设该容器的建造费用仅与其表面积有关.已知圆柱形部分每平方米建造费用为3千元,半球形部分每平方米建造费用为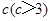 .设该容器的建造费用为
.设该容器的建造费用为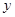 千元.
千元.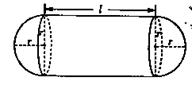
 关于
关于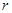 的函数表达式,并求该函数的定义域;
的函数表达式,并求该函数的定义域; ,其中
,其中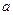 为大于零的常数.
为大于零的常数.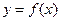 在点(1,
在点(1,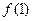 )处的切线与直线
)处的切线与直线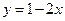 平行,求
平行,求 在区间[1,2]上的最小值.
在区间[1,2]上的最小值.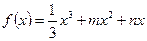 .
.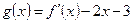 在
在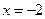 处取得最小值
处取得最小值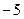 ,求
,求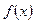 的解析式;
的解析式; ,
,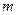 和
和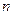
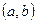 的长度为
的长度为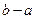 )
)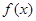 在定义域R内可导,若
在定义域R内可导,若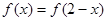 ,且当
,且当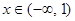 时,
时,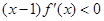 ,设
,设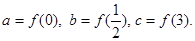 则( )
则( )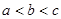
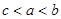
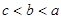

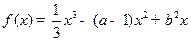 ,其中
,其中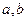 为常数.
为常数.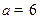 ,
,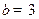 时,求函数
时,求函数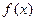 的单调递增区间;
的单调递增区间;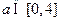 ,
,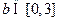 ,求函数
,求函数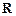 上是增函数的概率.
上是增函数的概率.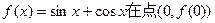 处的切线方程为
处的切线方程为