题目内容
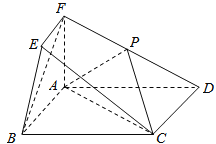
【题目】已知二面角α﹣l﹣β为60°,在其内部取点A,在半平面α,β内分别取点B,C.若点A到棱l的距离为1,则△ABC的周长的最小值为_____.
【答案】![]()
【解析】
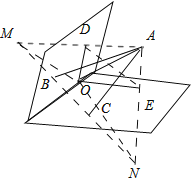
作A关于平面α和β的对称点M,N,交α和β与D,E,连接MN,AM,AN,DE,根据对称性三角形ADC的周长为AB+AC+BC=MB+BC+CN,当四点共线时长度最短,结合对称性和余弦定理求解.
作A关于平面α和β的对称点M,N,交α和β与D,E,
连接MN,AM,AN,DE,
根据对称性三角形ABC的周长为AB+AC+BC=MB+BC+CN,
当M,B,C,N共线时,周长最小为MN设平面ADE交l于,O,连接OD,OE,
显然OD⊥l,OE⊥l,
∠DOE=60°,∠MOA+∠AON=240°,OA=1,
∠MON=120°,且OM=ON=OA=1,根据余弦定理,
故MN2=1+1﹣2×1×1×cos120°=3,
故MN![]() .
.
故答案为:![]() .
.

练习册系列答案
 教学练新同步练习系列答案
教学练新同步练习系列答案 课前课后同步练习系列答案
课前课后同步练习系列答案 课堂小作业系列答案
课堂小作业系列答案 黄冈小状元口算速算练习册系列答案
黄冈小状元口算速算练习册系列答案 成功训练计划系列答案
成功训练计划系列答案 倍速训练法直通中考考点系列答案
倍速训练法直通中考考点系列答案
相关题目