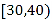题目内容
【题目】设点P是直线![]() 上一点,过点P分别作抛物线
上一点,过点P分别作抛物线![]() 的两条切线
的两条切线![]() ,其中A、B为切点.
,其中A、B为切点.
(1)若点A的坐标为![]() ,求点P的横坐标;
,求点P的横坐标;
(2)当![]() 的面积为
的面积为![]() 时,求
时,求![]() .
.
【答案】(1)![]() (2)
(2)![]()
【解析】
(1)由导数的几何意义,可先求直线切线![]() 的斜率
的斜率![]() ,由点斜式写出直线
,由点斜式写出直线![]() 方程,再由点
方程,再由点![]() 纵坐标为-2代入直线方程即可求解;
纵坐标为-2代入直线方程即可求解;
(2)设![]() ,分别表示出直线
,分别表示出直线![]() 的方程为
的方程为![]() ,同理得
,同理得![]() ,由两直线均过
,由两直线均过![]() 得
得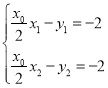 ,可推出直线方程为
,可推出直线方程为![]() ,联立抛物线方程
,联立抛物线方程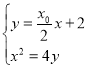 解出关于
解出关于![]() 的一元二次方程,结合弦长公式和点到直线距离公式表示出三角形面积公式为
的一元二次方程,结合弦长公式和点到直线距离公式表示出三角形面积公式为![]() ,即可求解
,即可求解![]() ,进而求解弦长
,进而求解弦长![]() ;还可设
;还可设![]() ,将
,将![]() 两点纵坐标结合抛物线代换,表示出直线
两点纵坐标结合抛物线代换,表示出直线![]() 的方程为
的方程为![]() ,同理直线
,同理直线![]() 的方程为
的方程为![]() ,联立解得
,联立解得![]() ,故
,故![]() ,设直线
,设直线![]() 的方程为
的方程为![]() ,联立
,联立 ,推出参数
,推出参数![]() ,后续求解步骤同前一种解法
,后续求解步骤同前一种解法
(1)由![]() ,所以
,所以![]() ,
,
因为![]() ,
,
由导数的几何意义知,切线![]() 的斜率
的斜率![]() ,
,
所以切线![]() 的方程为
的方程为![]() ,即
,即![]() ,
,
又因为点P为直线![]() 与直线
与直线![]() 的公共点,
的公共点,
联立![]() 与
与![]() ,可得P点横坐标为
,可得P点横坐标为![]() .
.
(2)法一:不妨设![]() ,
,
由(1)可知![]() ,即直线
,即直线![]() 的方程为
的方程为![]() ,
,
即![]() ,同理可得
,同理可得![]()
因为切线![]() 均过点
均过点![]() ,所以
,所以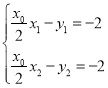 ,
,
所以![]() 为方程
为方程![]() 的两组解,
的两组解,
所以直线![]() 的方程为
的方程为![]() ,即
,即![]()
联立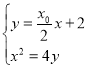 ,可得
,可得![]() ,显然
,显然![]() ,
,
由韦达定理得,![]() ,
,
所以 ,
,
又因为点P到直线![]() 的距离
的距离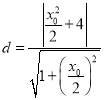 ,
,
所以 ,
,
解得![]() ,所以
,所以![]() .
.
法二:不妨设![]() ,由(1)可知直线
,由(1)可知直线![]() 的方程为
的方程为![]() ,
,
同理,直线![]() 的方程为
的方程为![]() ,
,
联立解得![]() ,
,
又点P在直线![]() ,所以
,所以![]() ,
,
设直线![]() 的方程为
的方程为![]() ,联立
,联立 ,可得
,可得![]() ,
,
由韦达定理得![]() ,
,
可得![]() ,
,
所以![]() ,
,
又因为点P到直线![]() 的距离为
的距离为 ,
,
所以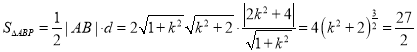 ,
,
解得![]() ,所以
,所以![]() .
.

练习册系列答案
 数学奥赛暑假天天练南京大学出版社系列答案
数学奥赛暑假天天练南京大学出版社系列答案 南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
相关题目