题目内容
(本小题满分14分)已知函数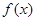 同时满足如下三个条件:①定义域为
同时满足如下三个条件:①定义域为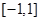 ;②
;②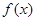 是偶函数;③
是偶函数;③ 时,
时,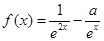 ,其中
,其中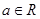 .
.
(Ⅰ)求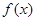 在
在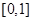 上的解析式,并求出函数
上的解析式,并求出函数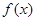 的最大值;
的最大值;
(Ⅱ)当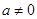 ,
,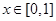 时,函数
时,函数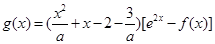 ,若
,若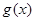 的图象恒在直线
的图象恒在直线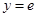 上方,求实数
上方,求实数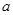 的取值范围(其中
的取值范围(其中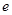 为自然对数的底数,
为自然对数的底数,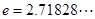 ).
).
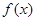 同时满足如下三个条件:①定义域为
同时满足如下三个条件:①定义域为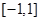 ;②
;②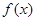 是偶函数;③
是偶函数;③ 时,
时,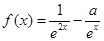 ,其中
,其中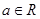 .
.(Ⅰ)求
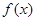 在
在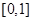 上的解析式,并求出函数
上的解析式,并求出函数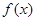 的最大值;
的最大值;(Ⅱ)当
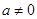 ,
,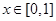 时,函数
时,函数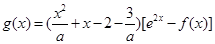 ,若
,若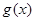 的图象恒在直线
的图象恒在直线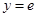 上方,求实数
上方,求实数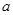 的取值范围(其中
的取值范围(其中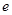 为自然对数的底数,
为自然对数的底数,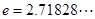 ).
).(Ⅰ)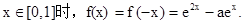
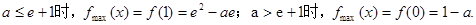
(Ⅱ)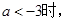
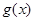 的图象恒在直线y=e上方
的图象恒在直线y=e上方
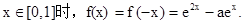
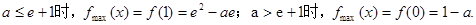
(Ⅱ)
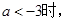
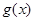 的图象恒在直线y=e上方
的图象恒在直线y=e上方本试题主要是考查了函数定义域和奇偶性的判定以及奇偶性的运用和解析式的求解,以及图像与图像的位置关系的运用。
(1)因为函数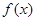 同时满足如下三个条件:①定义域为
同时满足如下三个条件:①定义域为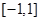 ;②
;②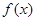 是偶函数;③
是偶函数;③ 时,
时,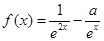 ,其中
,其中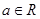 .
.
故可以得到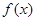 在
在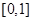 上的解析式,并求出函数
上的解析式,并求出函数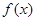 的最大值;
的最大值;
(2)当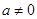 ,
,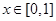 时,函数
时,函数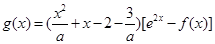 ,若
,若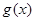 的图象恒在直线
的图象恒在直线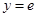 上方,即
上方,即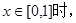
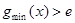 成立即可。
成立即可。
解:(Ⅰ)任取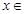
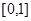 ,
,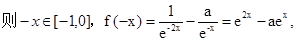
又f(x)是偶函数,故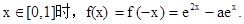 …………2分
…………2分
由f(x)是定义域为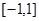 的偶函数可知,f(x)在
的偶函数可知,f(x)在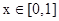 的最大值即可为f(x)的最大值.
的最大值即可为f(x)的最大值.
当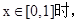

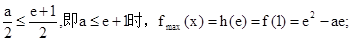
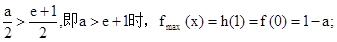 …………5分
…………5分
综上可知: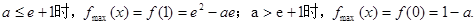
…………6分
另解:
由f(x)是定义域为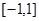 的偶函数可知,f(x)在
的偶函数可知,f(x)在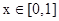 的最大值即可为f(x)的最大值.
的最大值即可为f(x)的最大值.
当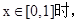
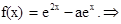
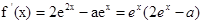
当
此时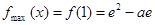 …
…
当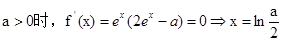
①当

此时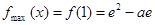
②当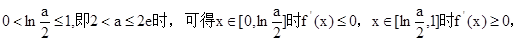
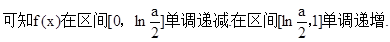
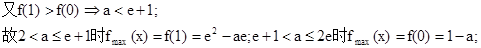
③
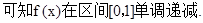
此时 …………7分
…………7分
综上可知: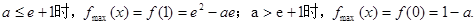
(2)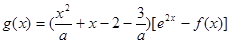
=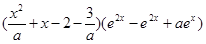 =
= …9分
…9分
要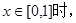 函数
函数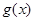 的图象恒在直线y=e上方,
的图象恒在直线y=e上方,
即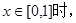
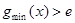 成立,…………10分
成立,…………10分
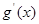
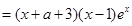 ,令
,令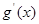 =0,解得
=0,解得
①当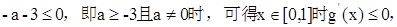
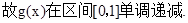
此时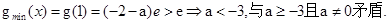 …………11分
…………11分
②当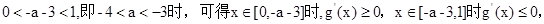
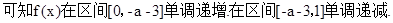 此时
此时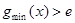
 ,
,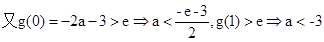
故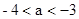 时可满足题意;…………12分
时可满足题意;…………12分
③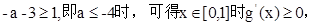
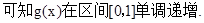
此时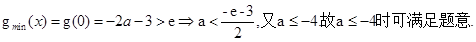 …13分
…13分
综上可知: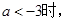
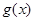 的图象恒在直线y=e上方,…………14分
的图象恒在直线y=e上方,…………14分
(1)因为函数
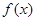 同时满足如下三个条件:①定义域为
同时满足如下三个条件:①定义域为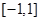 ;②
;②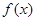 是偶函数;③
是偶函数;③ 时,
时,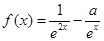 ,其中
,其中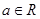 .
.故可以得到
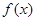 在
在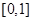 上的解析式,并求出函数
上的解析式,并求出函数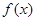 的最大值;
的最大值;(2)当
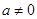 ,
,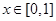 时,函数
时,函数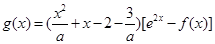 ,若
,若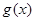 的图象恒在直线
的图象恒在直线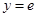 上方,即
上方,即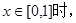
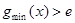 成立即可。
成立即可。解:(Ⅰ)任取
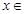
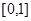 ,
,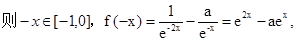
又f(x)是偶函数,故
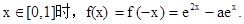 …………2分
…………2分由f(x)是定义域为
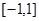 的偶函数可知,f(x)在
的偶函数可知,f(x)在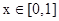 的最大值即可为f(x)的最大值.
的最大值即可为f(x)的最大值.当
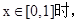

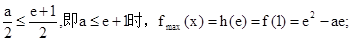
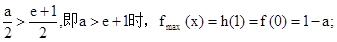 …………5分
…………5分综上可知:
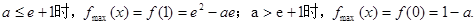
…………6分
另解:
由f(x)是定义域为
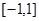 的偶函数可知,f(x)在
的偶函数可知,f(x)在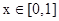 的最大值即可为f(x)的最大值.
的最大值即可为f(x)的最大值.当
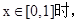
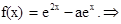
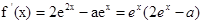
当

此时
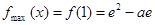 …
…当
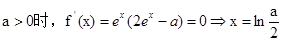
①当


此时
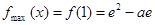
②当
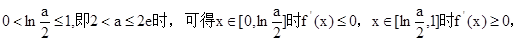
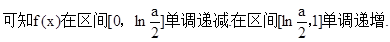
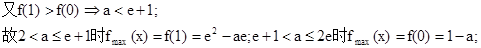
③

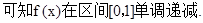
此时
 …………7分
…………7分综上可知:
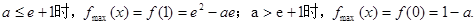
(2)
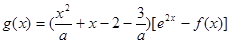
=
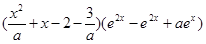 =
= …9分
…9分要
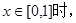 函数
函数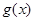 的图象恒在直线y=e上方,
的图象恒在直线y=e上方,即
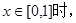
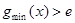 成立,…………10分
成立,…………10分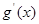
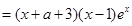 ,令
,令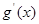 =0,解得
=0,解得①当
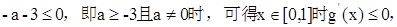
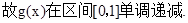
此时
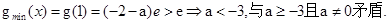 …………11分
…………11分②当
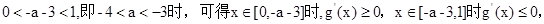
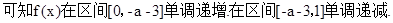 此时
此时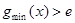
 ,
,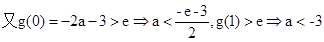
故
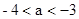 时可满足题意;…………12分
时可满足题意;…………12分③
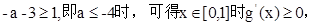
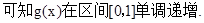
此时
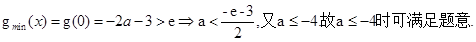 …13分
…13分综上可知:
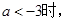
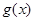 的图象恒在直线y=e上方,…………14分
的图象恒在直线y=e上方,…………14分
练习册系列答案
 时刻准备着暑假作业原子能出版社系列答案
时刻准备着暑假作业原子能出版社系列答案 暑假衔接教材期末暑假预习武汉出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案 假期作业暑假成长乐园新疆青少年出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案
相关题目
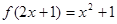 ,则
,则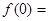 _______________.
_______________.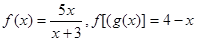 ,
,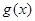 的解析式;
的解析式;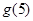 的值。
的值。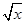 )2
)2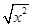
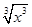
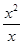
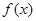 是定义域为
是定义域为 的偶函数,当
的偶函数,当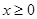 时,
时, ,则当
,则当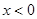 时,
时,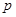 元(即税率为
元(即税率为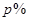 ),因此每年销量将减少
),因此每年销量将减少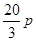 万件.
万件.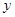 (万元),表示成
(万元),表示成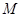 是满足下列性质函数的
是满足下列性质函数的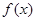 的全体,在定义域
的全体,在定义域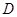 内存在
内存在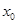 ,使得
,使得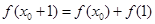 成立。(1)函数
成立。(1)函数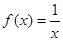 ,
,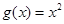 是否属于集合
是否属于集合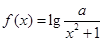 属于集合
属于集合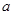 的取值范围。
的取值范围。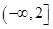 ,
,