��Ŀ����
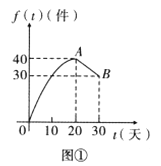
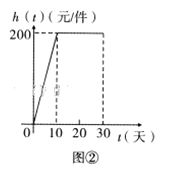
����Ŀ��ij�̳�Ԥ��ȫ���������ÿ̨��ֵ2000Ԫ�ĵ��ӻ���3600̨��ÿ�������̨����ͬ����ÿ�����븶�˷�400Ԫ�����湺��ĵ��ӻ�ȫ���������ܷ���ÿ��������ӻ����ܼ�ֵ�������˷ѣ������ȣ���ÿ������400̨����ȫ������ȥ�˷Ѻͱ��ܷ�43600Ԫ������ȫ��ֻ��24000Ԫ������֧���˷Ѻͱ��ܷѣ������ܷ�ǡ������ÿ��������������ʹ��24000Ԫ���ʽ��ã�д����Ľ��ۣ���˵�����ɣ�
���𰸡��⣺��ȫ������ȥ���˷Ѻͱ��ܷѵ��ܷ���ΪyԪ�����еı���ϵ����Ϊk��ÿ������x̨������� ![]() ����
����
ÿ������2000xԪ��
������֪y= ![]() ��400+2000kx��
��400+2000kx��
��x=400ʱ��y=43600��
���k= ![]()
��y= ![]() ��400+100x��2
��400+100x��2 ![]() =24000��Ԫ��
=24000��Ԫ��
���ҽ��� ![]() ��400=100x����x=120ʱ�Ⱥų�����
��400=100x����x=120ʱ�Ⱥų�����
��ʱx=120̨��ȫ�깲��Ҫ�ʽ�24000Ԫ��
��ֻ��ÿ������120̨������ʹ�ʽ���
���������������������˷Ѻͱ��ܷѵ��ܷ���y����ÿ������̨��x�ĺ�������ʽ��Ȼ�����û�������ʽ���н��
�����㾫����������Ҫ�����˻�������ʽ����ֵ�����е�Ӧ�õ����֪ʶ�㣬��Ҫ�����û�������ʽ����ֵʱ����������С���Ͷ������Ҫע����������������һ��������������ȡ�������ȷ�����⣮

 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�