题目内容
14.已知函数f(x)=2cos$\frac{x}{2}$($\sqrt{3}$cos$\frac{x}{2}$-sin$\frac{x}{2}$),在△ABC中,∠A、∠B、∠C的对边分别是a、b、c且f(C)=$\sqrt{3}$+1.(1)求∠C的大小;
(2)若c=2,且△ABC的面积为2$\sqrt{3}$,求cos2A+cos2B的值.
分析 (1)运用解析式得出cos(C$+\frac{π}{6}$)=$\frac{1}{2}$,即可求解C=$\frac{π}{6}$,
(2)利用面积公式和余弦定理得出$\left\{\begin{array}{l}{ab=8\sqrt{3}}\\{{a}^{2}+{b}^{2}-\sqrt{3}ab=4}\end{array}\right.$解出a,b的值,再运用正弦定理得出sinB,sinA,最后运用三角公式求解即可.
解答 解:函数f(x)=2cos$\frac{x}{2}$($\sqrt{3}$cos$\frac{x}{2}$-sin$\frac{x}{2}$)=2$\sqrt{3}$cos2($\frac{x}{2}$)-sinx=2cos(x+$\frac{π}{6}$)$+\sqrt{3}$,
(1)∵在△ABC中f(C)=$\sqrt{3}$+1.
∴cos(C$+\frac{π}{6}$)=$\frac{1}{2}$,C=$\frac{π}{6}$,
(2)∵C=$\frac{π}{6}$,c=2,∴c2=a2+b2$-2ab×\frac{\sqrt{3}}{2}$,$\frac{ab}{2}$sinC=2$\sqrt{3}$,
∴$\left\{\begin{array}{l}{ab=8\sqrt{3}}\\{{a}^{2}+{b}^{2}-\sqrt{3}ab=4}\end{array}\right.$解得a=4,b=2$\sqrt{3}$或a=2$\sqrt{3}$,b=4,
$\frac{a}{sinA}$=$\frac{b}{sinB}$=$\frac{c}{sinC}$=2R,
∴R=2,a=4,b=2$\sqrt{3}$,sinA=1,sinB=$\frac{\sqrt{3}}{2}$或a=2$\sqrt{3}$,b=4,sinB=1,sinA=$\frac{\sqrt{3}}{2}$.
∴cos2A+cos2B=2-2(sin2A+sin2B)=2-2(1+$\frac{3}{4}$)=2-2×$\frac{7}{4}$=$-\frac{3}{2}$,另一种情况,计算得cos2A+cos2B=$\frac{9}{2}$>2,舍弃.
故cos2A+cos2B=$-\frac{3}{2}$.
点评 此题考查了正弦定理,二倍角的正弦、余弦函数公式,同角三角函数间基本关系的运用,正弦函数的定义域与值域,以及特殊角的三角函数值,熟练掌握定理及公式是解本题的关键

 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案 普通高中同步练习册系列答案
普通高中同步练习册系列答案| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
 如图所示,已知四棱锥的侧棱PD⊥平面ABCD,且底面ABCD是直角梯形,AD⊥CD,AB∥CD,AB=AD=$\frac{1}{2}$CD=2,点M是侧棱PC的中点.
如图所示,已知四棱锥的侧棱PD⊥平面ABCD,且底面ABCD是直角梯形,AD⊥CD,AB∥CD,AB=AD=$\frac{1}{2}$CD=2,点M是侧棱PC的中点.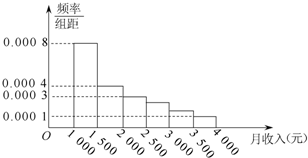 如图是某市有关部门根据该市干部的月收入情况,作抽样调查后画出的样本频率分布直方图.已知图中第一组的频数为4000,请根据该图提供的信息 (图中每组包括左端点,不包括右端点,如第一组表示收入在[1000,1500)),回答:
如图是某市有关部门根据该市干部的月收入情况,作抽样调查后画出的样本频率分布直方图.已知图中第一组的频数为4000,请根据该图提供的信息 (图中每组包括左端点,不包括右端点,如第一组表示收入在[1000,1500)),回答: